Question Number 92691 by john santu last updated on 08/May/20
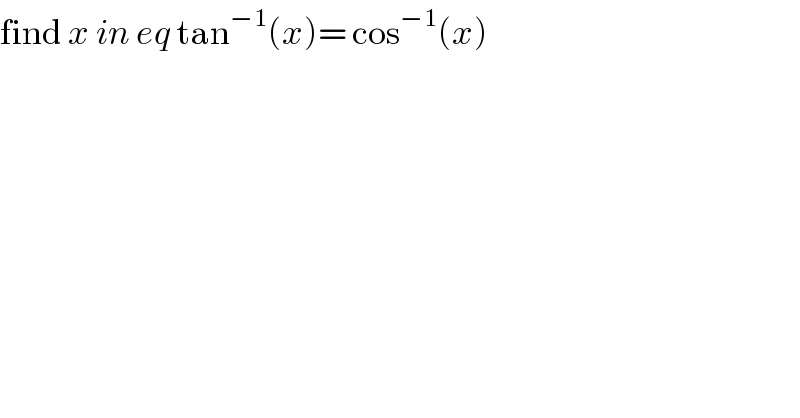
$$\mathrm{find}\:{x}\:{in}\:{eq}\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)=\:\mathrm{cos}^{−\mathrm{1}} \left({x}\right) \\ $$
Commented by Prithwish Sen 1 last updated on 08/May/20
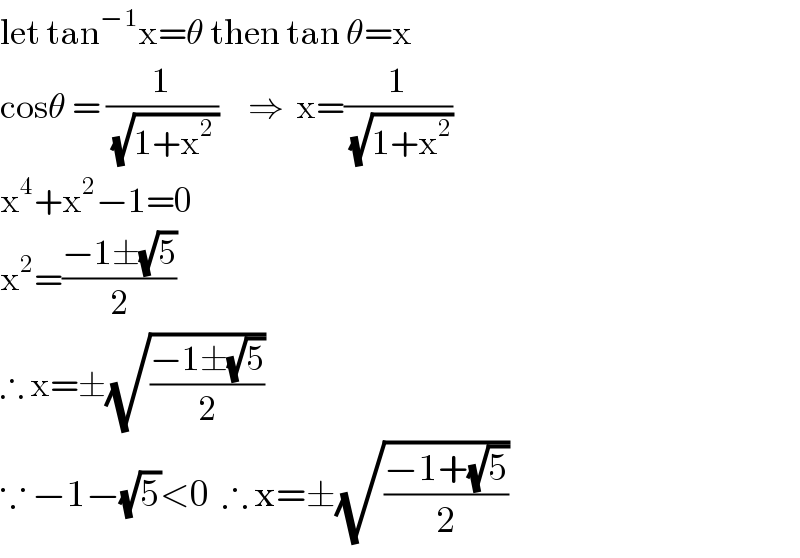
$$\mathrm{let}\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x}=\theta\:\mathrm{then}\:\mathrm{tan}\:\theta=\mathrm{x} \\ $$$$\mathrm{cos}\theta\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}\:} }}\:\:\:\:\:\Rightarrow\:\:\mathrm{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} =\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\therefore\:\mathrm{x}=\pm\sqrt{\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}} \\ $$$$\because\:−\mathrm{1}−\sqrt{\mathrm{5}}<\mathrm{0}\:\:\therefore\:\mathrm{x}=\pm\sqrt{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}} \\ $$
Commented by mr W last updated on 08/May/20
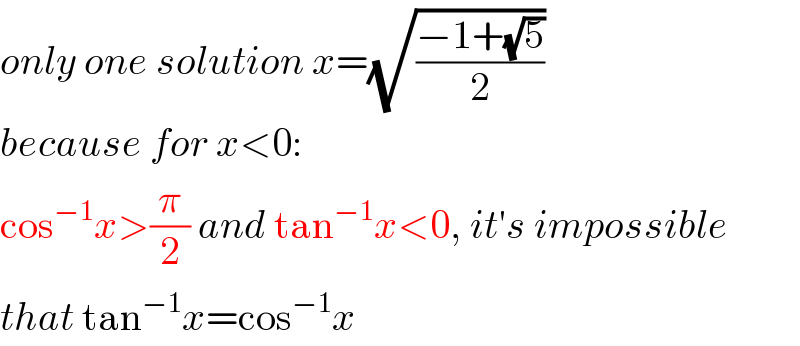
$${only}\:{one}\:{solution}\:{x}=\sqrt{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}} \\ $$$${because}\:{for}\:{x}<\mathrm{0}: \\ $$$$\mathrm{cos}^{−\mathrm{1}} {x}>\frac{\pi}{\mathrm{2}}\:{and}\:\mathrm{tan}^{−\mathrm{1}} {x}<\mathrm{0},\:{it}'{s}\:{impossible} \\ $$$${that}\:\mathrm{tan}^{−\mathrm{1}} {x}=\mathrm{cos}^{−\mathrm{1}} {x} \\ $$
Commented by Ar Brandon last updated on 08/May/20
OK, thanks for the clarification.
Answered by Ar Brandon last updated on 08/May/20
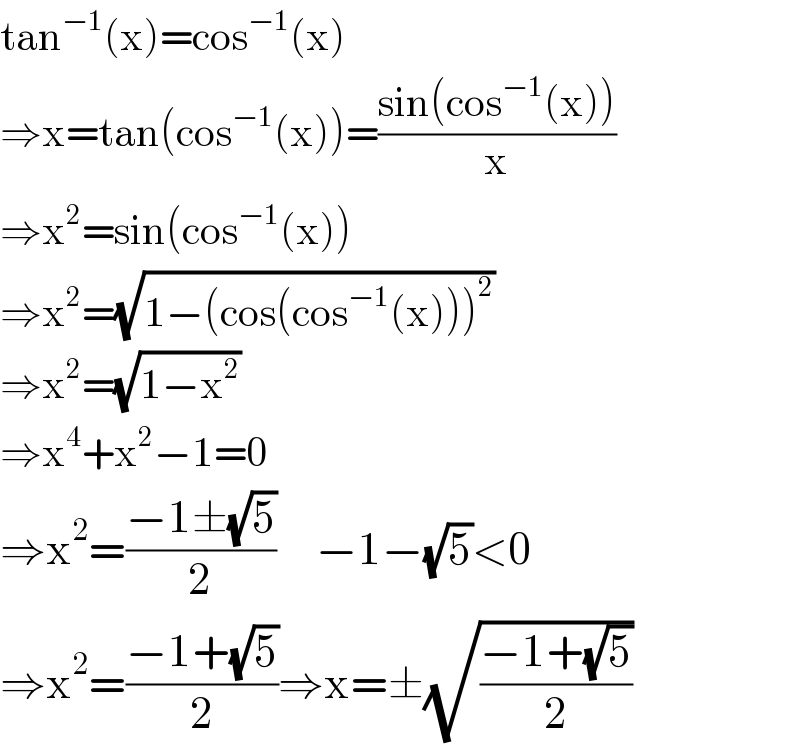
$$\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{x}=\mathrm{tan}\left(\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)=\frac{\mathrm{sin}\left(\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)}{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\mathrm{sin}\left(\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)\right) \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\sqrt{\mathrm{1}−\left(\mathrm{cos}\left(\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:\:\:\:−\mathrm{1}−\sqrt{\mathrm{5}}<\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow\mathrm{x}=\pm\sqrt{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}} \\ $$
