find-x-in-x-2-5-x-2-19-

Question Number 110856 by mathdave last updated on 31/Aug/20

$${find}\:{x}\:{in}\: \\ $$$${x}^{\mathrm{2}} =\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{19} \\ $$

Answered by mr W last updated on 31/Aug/20

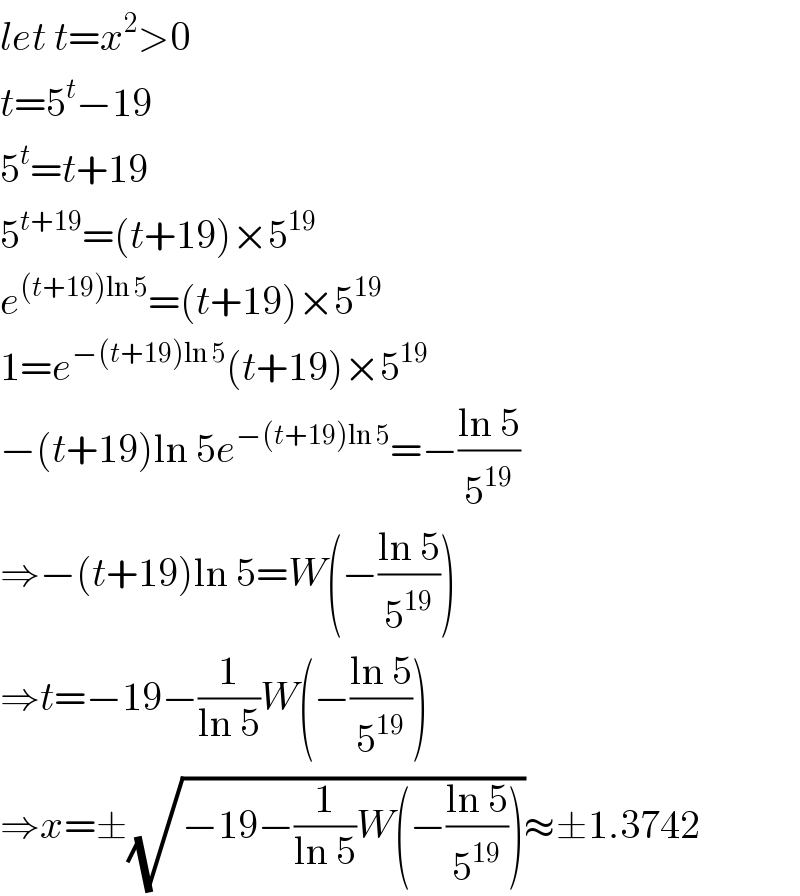
let t=x^2 >0 t=5^t −19 5^t =t+19 5^(t+19) =(t+19)×5^(19) e^((t+19)ln 5) =(t+19)×5^(19) 1=e^(−(t+19)ln 5) (t+19)×5^(19) −(t+19)ln 5e^(−(t+19)ln 5) =−((ln 5)/5^(19) ) ⇒−(t+19)ln 5=W(−((ln 5)/5^(19) )) ⇒t=−19−(1/(ln 5))W(−((ln 5)/5^(19) )) ⇒x=±(√(−19−(1/(ln 5))W(−((ln 5)/5^(19) ))))≈±1.3742

$${let}\:{t}={x}^{\mathrm{2}} >\mathrm{0} \\ $$$${t}=\mathrm{5}^{{t}} −\mathrm{19} \\ $$$$\mathrm{5}^{{t}} ={t}+\mathrm{19} \\ $$$$\mathrm{5}^{{t}+\mathrm{19}} =\left({t}+\mathrm{19}\right)×\mathrm{5}^{\mathrm{19}} \\ $$$${e}^{\left({t}+\mathrm{19}\right)\mathrm{ln}\:\mathrm{5}} =\left({t}+\mathrm{19}\right)×\mathrm{5}^{\mathrm{19}} \\ $$$$\mathrm{1}={e}^{−\left({t}+\mathrm{19}\right)\mathrm{ln}\:\mathrm{5}} \left({t}+\mathrm{19}\right)×\mathrm{5}^{\mathrm{19}} \\ $$$$−\left({t}+\mathrm{19}\right)\mathrm{ln}\:\mathrm{5}{e}^{−\left({t}+\mathrm{19}\right)\mathrm{ln}\:\mathrm{5}} =−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}^{\mathrm{19}} } \\ $$$$\Rightarrow−\left({t}+\mathrm{19}\right)\mathrm{ln}\:\mathrm{5}={W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}^{\mathrm{19}} }\right) \\ $$$$\Rightarrow{t}=−\mathrm{19}−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{5}}{W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}^{\mathrm{19}} }\right) \\ $$$$\Rightarrow{x}=\pm\sqrt{−\mathrm{19}−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{5}}{W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}^{\mathrm{19}} }\right)}\approx\pm\mathrm{1}.\mathrm{3742} \\ $$

Commented by mathdave last updated on 31/Aug/20

$${perfect}\:{solution} \\ $$

Answered by Dwaipayan Shikari last updated on 31/Aug/20

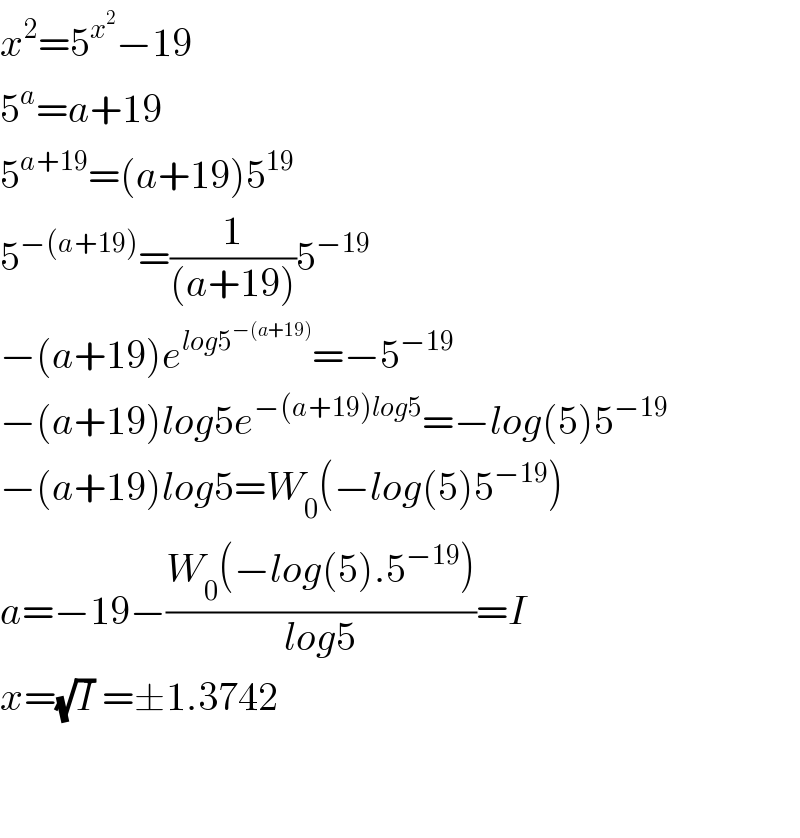
x^2 =5^x^2 −19 5^a =a+19 5^(a+19) =(a+19)5^(19) 5^(−(a+19)) =(1/((a+19)))5^(−19) −(a+19)e^(log5^(−(a+19)) ) =−5^(−19) −(a+19)log5e^(−(a+19)log5) =−log(5)5^(−19) −(a+19)log5=W_0 (−log(5)5^(−19) ) a=−19−((W_0 (−log(5).5^(−19) ))/(log5))=I x=(√I) =±1.3742

$${x}^{\mathrm{2}} =\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{19} \\ $$$$\mathrm{5}^{{a}} ={a}+\mathrm{19} \\ $$$$\mathrm{5}^{{a}+\mathrm{19}} =\left({a}+\mathrm{19}\right)\mathrm{5}^{\mathrm{19}} \\ $$$$\mathrm{5}^{−\left({a}+\mathrm{19}\right)} =\frac{\mathrm{1}}{\left({a}+\mathrm{19}\right)}\mathrm{5}^{−\mathrm{19}} \\ $$$$−\left({a}+\mathrm{19}\right){e}^{{log}\mathrm{5}^{−\left({a}+\mathrm{19}\right)} } =−\mathrm{5}^{−\mathrm{19}} \\ $$$$−\left({a}+\mathrm{19}\right){log}\mathrm{5}{e}^{−\left({a}+\mathrm{19}\right){log}\mathrm{5}} =−{log}\left(\mathrm{5}\right)\mathrm{5}^{−\mathrm{19}} \\ $$$$−\left({a}+\mathrm{19}\right){log}\mathrm{5}={W}_{\mathrm{0}} \left(−{log}\left(\mathrm{5}\right)\mathrm{5}^{−\mathrm{19}} \right) \\ $$$${a}=−\mathrm{19}−\frac{{W}_{\mathrm{0}} \left(−{log}\left(\mathrm{5}\right).\mathrm{5}^{−\mathrm{19}} \right)}{{log}\mathrm{5}}={I} \\ $$$${x}=\sqrt{{I}}\:=\pm\mathrm{1}.\mathrm{3742} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

find-x-in-x-2-5-x-2-19-

Leave a Reply Cancel reply