Question Number 157805 by Huy last updated on 28/Oct/21
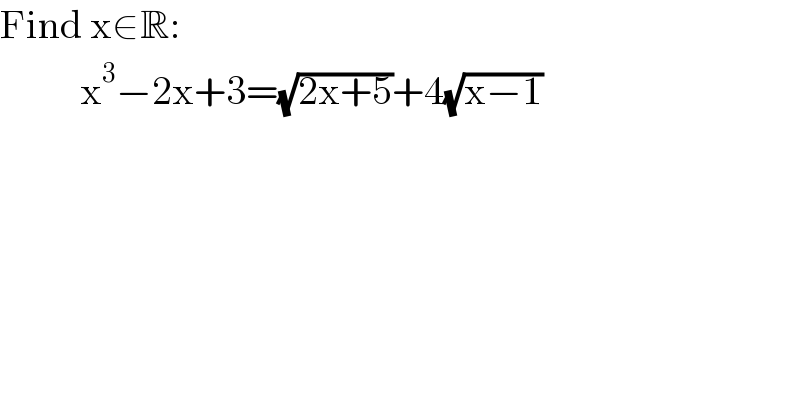
$$\mathrm{Find}\:\mathrm{x}\in\mathbb{R}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{3}} −\mathrm{2x}+\mathrm{3}=\sqrt{\mathrm{2x}+\mathrm{5}}+\mathrm{4}\sqrt{\mathrm{x}−\mathrm{1}} \\ $$
Answered by MJS_new last updated on 28/Oct/21
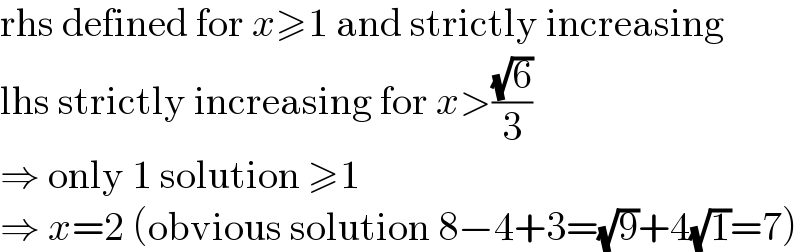
$$\mathrm{rhs}\:\mathrm{defined}\:\mathrm{for}\:{x}\geqslant\mathrm{1}\:\mathrm{and}\:\mathrm{strictly}\:\mathrm{increasing} \\ $$$$\mathrm{lhs}\:\mathrm{strictly}\:\mathrm{increasing}\:\mathrm{for}\:{x}>\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{only}\:\mathrm{1}\:\mathrm{solution}\:\geqslant\mathrm{1} \\ $$$$\Rightarrow\:{x}=\mathrm{2}\:\left(\mathrm{obvious}\:\mathrm{solution}\:\mathrm{8}−\mathrm{4}+\mathrm{3}=\sqrt{\mathrm{9}}+\mathrm{4}\sqrt{\mathrm{1}}=\mathrm{7}\right) \\ $$
