Menu Close

find-x-x-4-x-3-19x-2-93x-128-0-

Tinku Tara 0 Comments
Pin




Question Number 183746 by ali009 last updated on 29/Dec/22
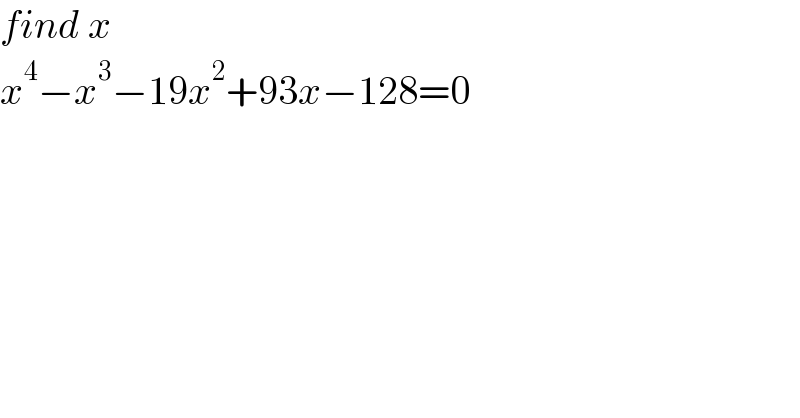
find x x^4 −x^3 −19x^2 +93x−128=0
$${find}\:{x} \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\mathrm{19}{x}^{\mathrm{2}} +\mathrm{93}{x}−\mathrm{128}=\mathrm{0} \\ $$
Commented by Frix last updated on 29/Dec/22
No useable exact solution, you can only approximate.
$$\mathrm{No}\:\mathrm{useable}\:\mathrm{exact}\:\mathrm{solution},\:\mathrm{you}\:\mathrm{can}\:\mathrm{only} \\ $$$$\mathrm{approximate}. \\ $$
Commented by Michaelfaraday last updated on 29/Dec/22
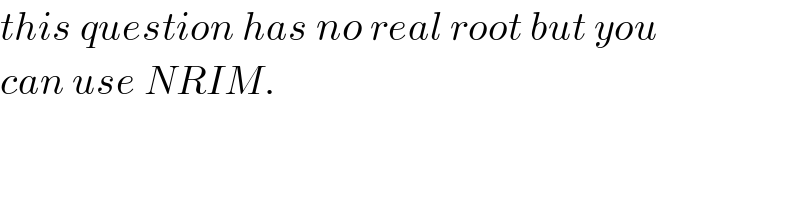
this question has no real root but you can use NRIM.
$${this}\:{question}\:{has}\:{no}\:{real}\:{root}\:{but}\:{you}\: \\ $$$${can}\:{use}\:{NRIM}. \\ $$$$ \\ $$
Commented by mr W last updated on 30/Dec/22
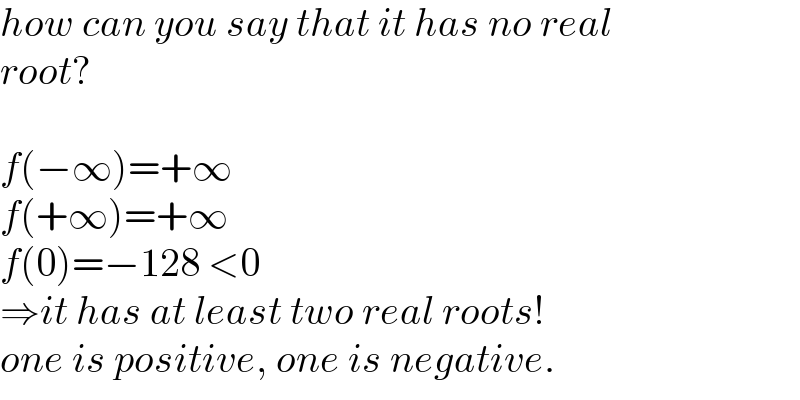
how can you say that it has no real root? f(−∞)=+∞ f(+∞)=+∞ f(0)=−128 <0 ⇒it has at least two real roots! one is positive, one is negative.
$${how}\:{can}\:{you}\:{say}\:{that}\:{it}\:{has}\:{no}\:{real} \\ $$$${root}? \\ $$$$ \\ $$$${f}\left(−\infty\right)=+\infty \\ $$$${f}\left(+\infty\right)=+\infty \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{128}\:<\mathrm{0} \\ $$$$\Rightarrow{it}\:{has}\:{at}\:{least}\:{two}\:{real}\:{roots}! \\ $$$${one}\:{is}\:{positive},\:{one}\:{is}\:{negative}. \\ $$
Commented by Michaelfaraday last updated on 30/Dec/22
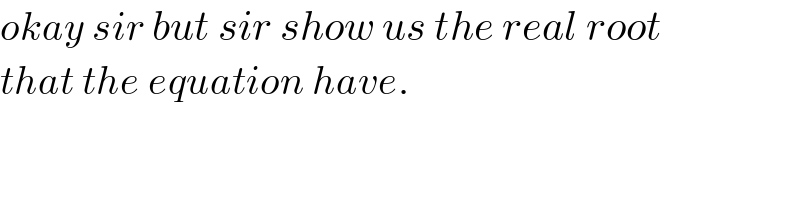
okay sir but sir show us the real root that the equation have.
$${okay}\:{sir}\:{but}\:{sir}\:{show}\:{us}\:{the}\:{real}\:{root} \\ $$$${that}\:{the}\:{equation}\:{have}. \\ $$
Commented by MJS_new last updated on 30/Dec/22
x_1 ≈−5.76397627403 x_2 ≈2.26841847295 x_(3, 4) ≈2.24777890054±2.17648395669i
$${x}_{\mathrm{1}} \approx−\mathrm{5}.\mathrm{76397627403} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{2}.\mathrm{26841847295} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} \approx\mathrm{2}.\mathrm{24777890054}\pm\mathrm{2}.\mathrm{17648395669i} \\ $$
Answered by aleks041103 last updated on 29/Dec/22
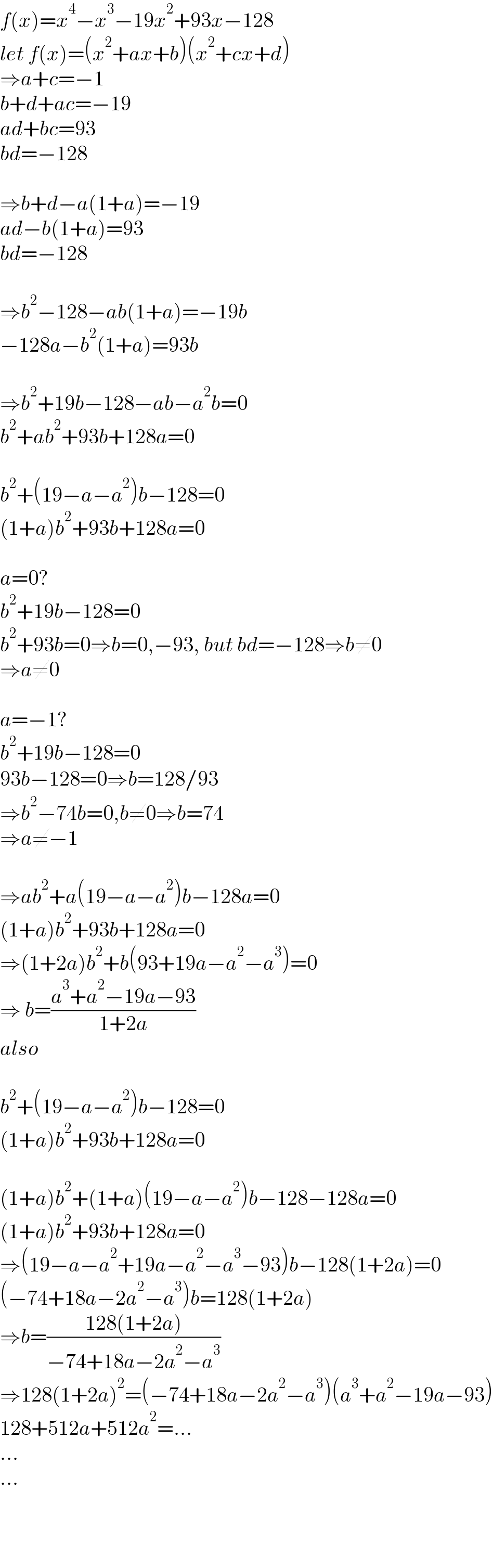
f(x)=x^4 −x^3 −19x^2 +93x−128 let f(x)=(x^2 +ax+b)(x^2 +cx+d) ⇒a+c=−1 b+d+ac=−19 ad+bc=93 bd=−128 ⇒b+d−a(1+a)=−19 ad−b(1+a)=93 bd=−128 ⇒b^2 −128−ab(1+a)=−19b −128a−b^2 (1+a)=93b ⇒b^2 +19b−128−ab−a^2 b=0 b^2 +ab^2 +93b+128a=0 b^2 +(19−a−a^2 )b−128=0 (1+a)b^2 +93b+128a=0 a=0? b^2 +19b−128=0 b^2 +93b=0⇒b=0,−93, but bd=−128⇒b≠0 ⇒a≠0 a=−1? b^2 +19b−128=0 93b−128=0⇒b=128/93 ⇒b^2 −74b=0,b≠0⇒b=74 ⇒a≠−1 ⇒ab^2 +a(19−a−a^2 )b−128a=0 (1+a)b^2 +93b+128a=0 ⇒(1+2a)b^2 +b(93+19a−a^2 −a^3 )=0 ⇒ b=((a^3 +a^2 −19a−93)/(1+2a)) also b^2 +(19−a−a^2 )b−128=0 (1+a)b^2 +93b+128a=0 (1+a)b^2 +(1+a)(19−a−a^2 )b−128−128a=0 (1+a)b^2 +93b+128a=0 ⇒(19−a−a^2 +19a−a^2 −a^3 −93)b−128(1+2a)=0 (−74+18a−2a^2 −a^3 )b=128(1+2a) ⇒b=((128(1+2a))/(−74+18a−2a^2 −a^3 )) ⇒128(1+2a)^2 =(−74+18a−2a^2 −a^3 )(a^3 +a^2 −19a−93) 128+512a+512a^2 =... ... ...
$${f}\left({x}\right)={x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\mathrm{19}{x}^{\mathrm{2}} +\mathrm{93}{x}−\mathrm{128} \\ $$$${let}\:{f}\left({x}\right)=\left({x}^{\mathrm{2}} +{ax}+{b}\right)\left({x}^{\mathrm{2}} +{cx}+{d}\right) \\ $$$$\Rightarrow{a}+{c}=−\mathrm{1} \\ $$$${b}+{d}+{ac}=−\mathrm{19} \\ $$$${ad}+{bc}=\mathrm{93} \\ $$$${bd}=−\mathrm{128} \\ $$$$ \\ $$$$\Rightarrow{b}+{d}−{a}\left(\mathrm{1}+{a}\right)=−\mathrm{19} \\ $$$${ad}−{b}\left(\mathrm{1}+{a}\right)=\mathrm{93} \\ $$$${bd}=−\mathrm{128} \\ $$$$ \\ $$$$\Rightarrow{b}^{\mathrm{2}} −\mathrm{128}−{ab}\left(\mathrm{1}+{a}\right)=−\mathrm{19}{b} \\ $$$$−\mathrm{128}{a}−{b}^{\mathrm{2}} \left(\mathrm{1}+{a}\right)=\mathrm{93}{b} \\ $$$$ \\ $$$$\Rightarrow{b}^{\mathrm{2}} +\mathrm{19}{b}−\mathrm{128}−{ab}−{a}^{\mathrm{2}} {b}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} +{ab}^{\mathrm{2}} +\mathrm{93}{b}+\mathrm{128}{a}=\mathrm{0} \\ $$$$ \\ $$$${b}^{\mathrm{2}} +\left(\mathrm{19}−{a}−{a}^{\mathrm{2}} \right){b}−\mathrm{128}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{a}\right){b}^{\mathrm{2}} +\mathrm{93}{b}+\mathrm{128}{a}=\mathrm{0} \\ $$$$ \\ $$$${a}=\mathrm{0}? \\ $$$${b}^{\mathrm{2}} +\mathrm{19}{b}−\mathrm{128}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} +\mathrm{93}{b}=\mathrm{0}\Rightarrow{b}=\mathrm{0},−\mathrm{93},\:{but}\:{bd}=−\mathrm{128}\Rightarrow{b}\neq\mathrm{0} \\ $$$$\Rightarrow{a}\neq\mathrm{0} \\ $$$$ \\ $$$${a}=−\mathrm{1}? \\ $$$${b}^{\mathrm{2}} +\mathrm{19}{b}−\mathrm{128}=\mathrm{0} \\ $$$$\mathrm{93}{b}−\mathrm{128}=\mathrm{0}\Rightarrow{b}=\mathrm{128}/\mathrm{93} \\ $$$$\Rightarrow{b}^{\mathrm{2}} −\mathrm{74}{b}=\mathrm{0},{b}\neq\mathrm{0}\Rightarrow{b}=\mathrm{74} \\ $$$$\Rightarrow{a}\neq−\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{ab}^{\mathrm{2}} +{a}\left(\mathrm{19}−{a}−{a}^{\mathrm{2}} \right){b}−\mathrm{128}{a}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{a}\right){b}^{\mathrm{2}} +\mathrm{93}{b}+\mathrm{128}{a}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{2}{a}\right){b}^{\mathrm{2}} +{b}\left(\mathrm{93}+\mathrm{19}{a}−{a}^{\mathrm{2}} −{a}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:{b}=\frac{{a}^{\mathrm{3}} +{a}^{\mathrm{2}} −\mathrm{19}{a}−\mathrm{93}}{\mathrm{1}+\mathrm{2}{a}} \\ $$$${also} \\ $$$$ \\ $$$${b}^{\mathrm{2}} +\left(\mathrm{19}−{a}−{a}^{\mathrm{2}} \right){b}−\mathrm{128}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{a}\right){b}^{\mathrm{2}} +\mathrm{93}{b}+\mathrm{128}{a}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{1}+{a}\right){b}^{\mathrm{2}} +\left(\mathrm{1}+{a}\right)\left(\mathrm{19}−{a}−{a}^{\mathrm{2}} \right){b}−\mathrm{128}−\mathrm{128}{a}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{a}\right){b}^{\mathrm{2}} +\mathrm{93}{b}+\mathrm{128}{a}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{19}−{a}−{a}^{\mathrm{2}} +\mathrm{19}{a}−{a}^{\mathrm{2}} −{a}^{\mathrm{3}} −\mathrm{93}\right){b}−\mathrm{128}\left(\mathrm{1}+\mathrm{2}{a}\right)=\mathrm{0} \\ $$$$\left(−\mathrm{74}+\mathrm{18}{a}−\mathrm{2}{a}^{\mathrm{2}} −{a}^{\mathrm{3}} \right){b}=\mathrm{128}\left(\mathrm{1}+\mathrm{2}{a}\right) \\ $$$$\Rightarrow{b}=\frac{\mathrm{128}\left(\mathrm{1}+\mathrm{2}{a}\right)}{−\mathrm{74}+\mathrm{18}{a}−\mathrm{2}{a}^{\mathrm{2}} −{a}^{\mathrm{3}} } \\ $$$$\Rightarrow\mathrm{128}\left(\mathrm{1}+\mathrm{2}{a}\right)^{\mathrm{2}} =\left(−\mathrm{74}+\mathrm{18}{a}−\mathrm{2}{a}^{\mathrm{2}} −{a}^{\mathrm{3}} \right)\left({a}^{\mathrm{3}} +{a}^{\mathrm{2}} −\mathrm{19}{a}−\mathrm{93}\right) \\ $$$$\mathrm{128}+\mathrm{512}{a}+\mathrm{512}{a}^{\mathrm{2}} =… \\ $$$$… \\ $$$$… \\ $$$$ \\ $$
Commented by Michaelfaraday last updated on 29/Dec/22
sir i dont understand your step?
$${sir}\:{i}\:{dont}\:{understand}\:{your}\:{step}? \\ $$
Commented by MJS_new last updated on 29/Dec/22
It′s not possible this way. x^4 +ax^3 +bx^2 +cx+d=0 1. let x=t−(a/4) to get t^4 +pt^2 +qt+r=0 2. now we might find 2 square factors (t^2 −αt+β)(t^2 +αt+γ)=0 by matching the constants. solve 2 of the 3 equations for β and γ, then insert in the 3^(rd) equation to get (α^2 )^3 +A(α^2 )^2 +Bα^2 +C=0 only if this has got “nice” solutions we get square factors we can work with.
$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{this}\:\mathrm{way}. \\ $$$${x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$$\mathrm{1}.\:\mathrm{let}\:{x}={t}−\frac{{a}}{\mathrm{4}}\:\mathrm{to}\:\mathrm{get} \\ $$$${t}^{\mathrm{4}} +{pt}^{\mathrm{2}} +{qt}+{r}=\mathrm{0} \\ $$$$\mathrm{2}.\:\mathrm{now}\:\mathrm{we}\:\mathrm{might}\:\mathrm{find}\:\mathrm{2}\:\mathrm{square}\:\mathrm{factors} \\ $$$$\left({t}^{\mathrm{2}} −\alpha{t}+\beta\right)\left({t}^{\mathrm{2}} +\alpha{t}+\gamma\right)=\mathrm{0} \\ $$$$\mathrm{by}\:\mathrm{matching}\:\mathrm{the}\:\mathrm{constants}. \\ $$$$\mathrm{solve}\:\mathrm{2}\:\mathrm{of}\:\mathrm{the}\:\mathrm{3}\:\mathrm{equations}\:\mathrm{for}\:\beta\:\mathrm{and}\:\gamma,\:\mathrm{then} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{equation}\:\mathrm{to}\:\mathrm{get} \\ $$$$\left(\alpha^{\mathrm{2}} \right)^{\mathrm{3}} +{A}\left(\alpha^{\mathrm{2}} \right)^{\mathrm{2}} +{B}\alpha^{\mathrm{2}} +{C}=\mathrm{0} \\ $$$$\mathrm{only}\:\mathrm{if}\:\mathrm{this}\:\mathrm{has}\:\mathrm{got}\:“\mathrm{nice}''\:\mathrm{solutions}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{square}\:\mathrm{factors}\:\mathrm{we}\:\mathrm{can}\:\mathrm{work}\:\mathrm{with}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *