Question Number 25000 by ErickDN last updated on 30/Nov/17
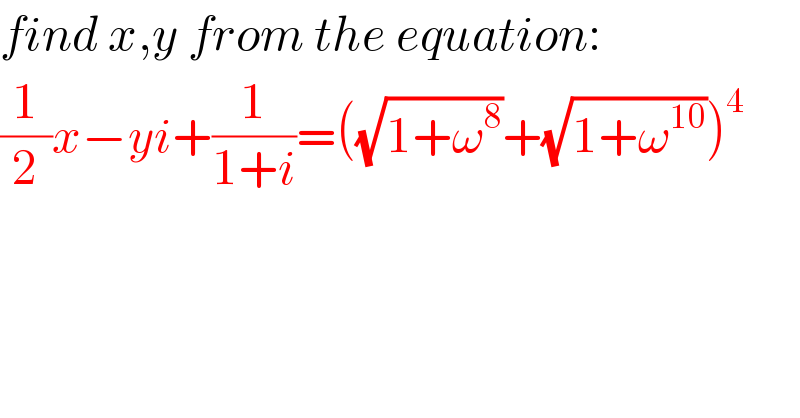
$${find}\:{x},{y}\:{from}\:{the}\:{equation}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{x}−{yi}+\frac{\mathrm{1}}{\mathrm{1}+{i}}=\left(\sqrt{\mathrm{1}+\omega^{\mathrm{8}} }+\sqrt{\mathrm{1}+\omega^{\mathrm{10}} }\right)^{\mathrm{4}} \\ $$$$ \\ $$
Answered by ajfour last updated on 01/Dec/17

$$\Rightarrow\:\:\frac{{x}}{\mathrm{2}}−{iy}+\frac{\mathrm{1}−{i}}{\mathrm{2}}=\left(\sqrt{−\omega}+\sqrt{−\omega^{\mathrm{2}} }\right)^{\mathrm{4}} \\ $$$$\frac{{x}}{\mathrm{2}}−{iy}=\frac{−\mathrm{1}+{i}}{\mathrm{2}}+\left({e}^{−\frac{{i}\pi}{\mathrm{6}}} +{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{4}} \\ $$$$\frac{{x}}{\mathrm{2}}−{iy}=\frac{−\mathrm{1}+{i}}{\mathrm{2}}+\mathrm{9} \\ $$$$\Rightarrow\:\:\:\:{x}=\mathrm{17}\:\:;\:\:{y}=−\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
