Menu Close

Find-x-y-R-such-that-x-y-x-2-xy-y-2-7-2-updated-from-2-7-7-2-Sorry-it-was-a-mistake-

Tinku Tara 0 Comments
Pin




Question Number 100240 by Ar Brandon last updated on 25/Jun/20
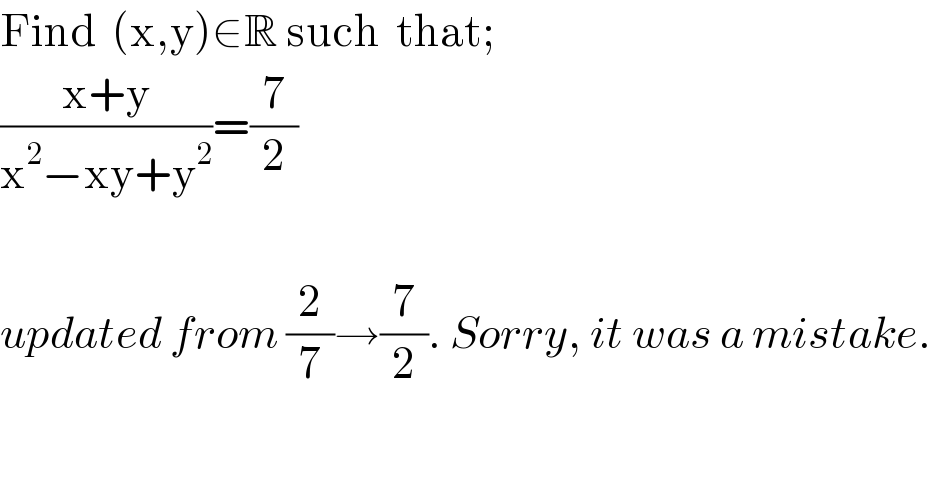
Find (x,y)∈R such that; ((x+y)/(x^2 −xy+y^2 ))=(7/2) updated from (2/7)→(7/2). Sorry, it was a mistake.
$$\mathrm{Find}\:\:\left(\mathrm{x},\mathrm{y}\right)\in\mathbb{R}\:\mathrm{such}\:\:\mathrm{that}; \\ $$$$\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$ \\ $$$${updated}\:{from}\:\frac{\mathrm{2}}{\mathrm{7}}\rightarrow\frac{\mathrm{7}}{\mathrm{2}}.\:{Sorry},\:{it}\:{was}\:{a}\:{mistake}. \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20
{x should be ±(1−(√2)) {y should be (√2)±1 x+y=2, x=2−y (x+y)^2 =7+3xy {Assuming} 4=7+3xy so xy=−1⇒(2−y)y=−1 ⇒y^2 −2y−1=0 ⇒y=((2±(√8))/2)=1±(√2) x(1±(√)2)=−1⇒x=((−1)/(1±(√2)))=(1±(√2)) {But it has infinite many solutions} If we go for all solutions x+y=2p {p≠0 and x^2 −xy+y^2 =7p (x+y)^2 =7p+3xy 4p^2 =7p+3xy xy=((4p^2 −7p)/3)⇒x(2p−x)=((4p^2 −7p)/3)⇒3x^2 −6px+4p^2 −7p=0 x=((6p±(√(36p^2 −48p^2 +84p)))/6)=((6p±(√(84p−12p^2 )))/6) And y=((8p^2 −14p)/(6p±(√(84p−12p^2 ))))
$$\left\{\mathrm{x}\:\mathrm{should}\:\mathrm{be}\:\pm\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)\right. \\ $$$$\left\{\mathrm{y}\:\mathrm{should}\:\mathrm{be}\:\sqrt{\mathrm{2}}\pm\mathrm{1}\right. \\ $$$$ \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{2},\:\:\mathrm{x}=\mathrm{2}−\mathrm{y} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{7}+\mathrm{3xy}\:\:\:\:\:\left\{\mathrm{Assuming}\right\} \\ $$$$\mathrm{4}=\mathrm{7}+\mathrm{3xy}\:\:\:\mathrm{so}\:\:\mathrm{xy}=−\mathrm{1}\Rightarrow\left(\mathrm{2}−\mathrm{y}\right)\mathrm{y}=−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{y}^{\mathrm{2}} −\mathrm{2y}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{y}=\frac{\mathrm{2}\pm\sqrt{\mathrm{8}}}{\mathrm{2}}=\mathrm{1}\pm\sqrt{\mathrm{2}} \\ $$$$\mathrm{x}\left(\mathrm{1}\pm\sqrt{}\mathrm{2}\right)=−\mathrm{1}\Rightarrow\mathrm{x}=\frac{−\mathrm{1}}{\mathrm{1}\pm\sqrt{\mathrm{2}}}=\left(\mathrm{1}\pm\sqrt{\mathrm{2}}\right) \\ $$$$ \\ $$$$\left\{\mathrm{But}\:\mathrm{it}\:\mathrm{has}\:\mathrm{infinite}\:\mathrm{many}\:\mathrm{solutions}\right\} \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{go}\:\mathrm{for}\:\mathrm{all}\:\mathrm{solutions} \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{2p}\:\:\left\{\mathrm{p}\neq\mathrm{0}\right. \\ $$$$\mathrm{and}\:\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{7p} \\ $$$$\:\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{7p}+\mathrm{3xy} \\ $$$$\:\:\mathrm{4p}^{\mathrm{2}} =\mathrm{7p}+\mathrm{3xy} \\ $$$$\:\:\mathrm{xy}=\frac{\mathrm{4p}^{\mathrm{2}} −\mathrm{7p}}{\mathrm{3}}\Rightarrow\mathrm{x}\left(\mathrm{2p}−\mathrm{x}\right)=\frac{\mathrm{4p}^{\mathrm{2}} −\mathrm{7p}}{\mathrm{3}}\Rightarrow\mathrm{3x}^{\mathrm{2}} −\mathrm{6px}+\mathrm{4p}^{\mathrm{2}} −\mathrm{7p}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\frac{\mathrm{6p}\pm\sqrt{\mathrm{36p}^{\mathrm{2}} −\mathrm{48p}^{\mathrm{2}} +\mathrm{84p}}}{\mathrm{6}}=\frac{\mathrm{6p}\pm\sqrt{\mathrm{84p}−\mathrm{12p}^{\mathrm{2}} }}{\mathrm{6}} \\ $$$$\mathrm{And}\:\:\:\mathrm{y}=\frac{\mathrm{8p}^{\mathrm{2}} −\mathrm{14p}}{\mathrm{6p}\pm\sqrt{\mathrm{84p}−\mathrm{12p}^{\mathrm{2}} }} \\ $$
Commented by mr W last updated on 25/Jun/20
the eqn. is an ellipse without the point(0,0). it has infinite points, i.e. infinite solutions.
$${the}\:{eqn}.\:{is}\:{an}\:{ellipse}\:{without}\:{the} \\ $$$${point}\left(\mathrm{0},\mathrm{0}\right).\:{it}\:{has}\:{infinite}\:{points}, \\ $$$${i}.{e}.\:{infinite}\:{solutions}. \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20
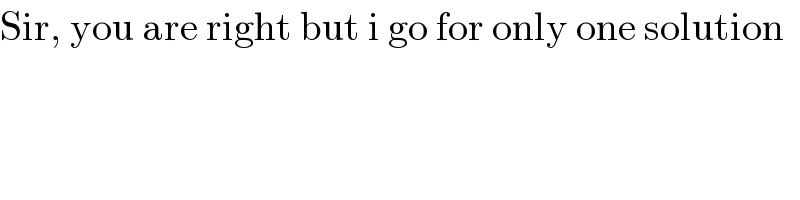
Sir, you are right but i go for only one solution
$$\mathrm{Sir},\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{but}\:\mathrm{i}\:\mathrm{go}\:\mathrm{for}\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution} \\ $$
Commented by mr W last updated on 25/Jun/20
Commented by mr W last updated on 25/Jun/20
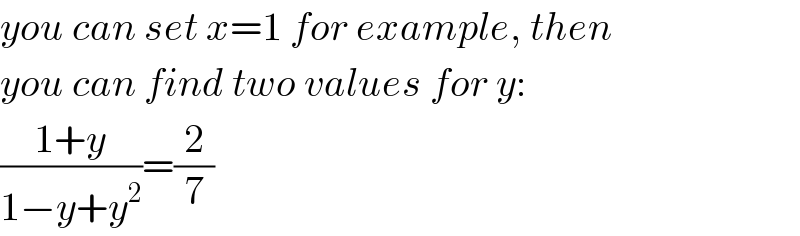
you can set x=1 for example, then you can find two values for y: ((1+y)/(1−y+y^2 ))=(2/7)
$${you}\:{can}\:{set}\:{x}=\mathrm{1}\:{for}\:{example},\:{then} \\ $$$${you}\:{can}\:{find}\:{two}\:{values}\:{for}\:{y}: \\ $$$$\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}+{y}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{7}} \\ $$
Commented by mr W last updated on 25/Jun/20
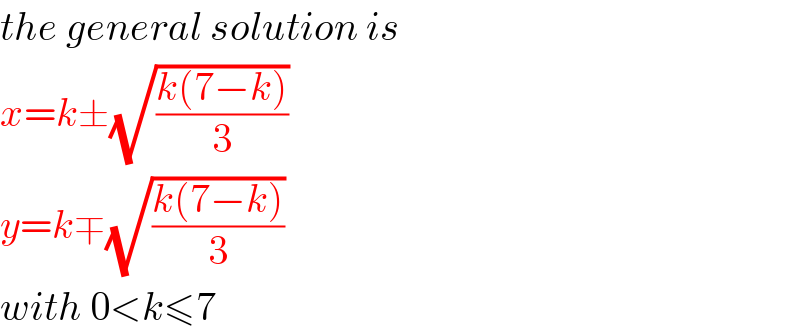
the general solution is x=k±(√((k(7−k))/3)) y=k∓(√((k(7−k))/3)) with 0<k≤7
$${the}\:{general}\:{solution}\:{is} \\ $$$${x}={k}\pm\sqrt{\frac{{k}\left(\mathrm{7}−{k}\right)}{\mathrm{3}}} \\ $$$${y}={k}\mp\sqrt{\frac{{k}\left(\mathrm{7}−{k}\right)}{\mathrm{3}}} \\ $$$${with}\:\mathrm{0}<{k}\leqslant\mathrm{7} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20
Yes sir i am a high school student .Thanking you for correction
$$\mathrm{Yes}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{am}\:\mathrm{a}\:\mathrm{high}\:\mathrm{school}\:\mathrm{student}\:.\mathrm{Thanking}\:\mathrm{you}\:\mathrm{for}\:\mathrm{correction} \\ $$
Commented by Ar Brandon last updated on 25/Jun/20
Thank you !
Commented by Ar Brandon last updated on 25/Jun/20
Thanks for your idea !
Answered by Ar Brandon last updated on 25/Jun/20
((x+y)/(x^2 −xy+y^2 ))=(7/2)⇒((x+y)/((x−(y/2))^2 −(y^2 /4)+y^2 ))=((x+y)/((x−(y/2))^2 +((3y^2 )/4)))=(7/2) ⇒ { ((x+y=7⇒x=7−y)),(((x−(y/2))^2 +((3y^2 )/4)=2)) :}⇒(7−y−(y/2))^2 +((3y^2 )/4)=2 ⇒(7−((3y)/2))^2 +((3y^2 )/4)=2⇒49−21y+((9y^2 )/4)+((3y^2 )/4)=2⇒3y^2 −21y+47=0 ⇒y=((21±(√(21^2 −4(3×47))))/(2(3)))=((21±(√(−123)))/6) I arrived at this, but it′s obvious that this isn′t correct, as y∉R. Anyone to help me out, please?
$$\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}}\Rightarrow\frac{\mathrm{x}+\mathrm{y}}{\left(\mathrm{x}−\frac{\mathrm{y}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{x}+\mathrm{y}}{\left(\mathrm{x}−\frac{\mathrm{y}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3y}^{\mathrm{2}} }{\mathrm{4}}}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{7}\Rightarrow\mathrm{x}=\mathrm{7}−\mathrm{y}}\\{\left(\mathrm{x}−\frac{\mathrm{y}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3y}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{2}}\end{cases}\Rightarrow\left(\mathrm{7}−\mathrm{y}−\frac{\mathrm{y}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3y}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{2} \\ $$$$\Rightarrow\left(\mathrm{7}−\frac{\mathrm{3y}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3y}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{2}\Rightarrow\mathrm{49}−\mathrm{21y}+\frac{\mathrm{9y}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{3y}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{2}\Rightarrow\mathrm{3y}^{\mathrm{2}} −\mathrm{21y}+\mathrm{47}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{21}\pm\sqrt{\mathrm{21}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{3}×\mathrm{47}\right)}}{\mathrm{2}\left(\mathrm{3}\right)}=\frac{\mathrm{21}\pm\sqrt{−\mathrm{123}}}{\mathrm{6}} \\ $$$$ \\ $$$${I}\:{arrived}\:{at}\:{this},\:{but}\:{it}'{s}\:{obvious}\:{that}\:{this}\:{isn}'{t}\: \\ $$$${correct},\:{as}\:{y}\notin\mathbb{R}.\:{Anyone}\:{to}\:{help}\:{me}\:{out},\:{please}? \\ $$
Commented by mr W last updated on 25/Jun/20
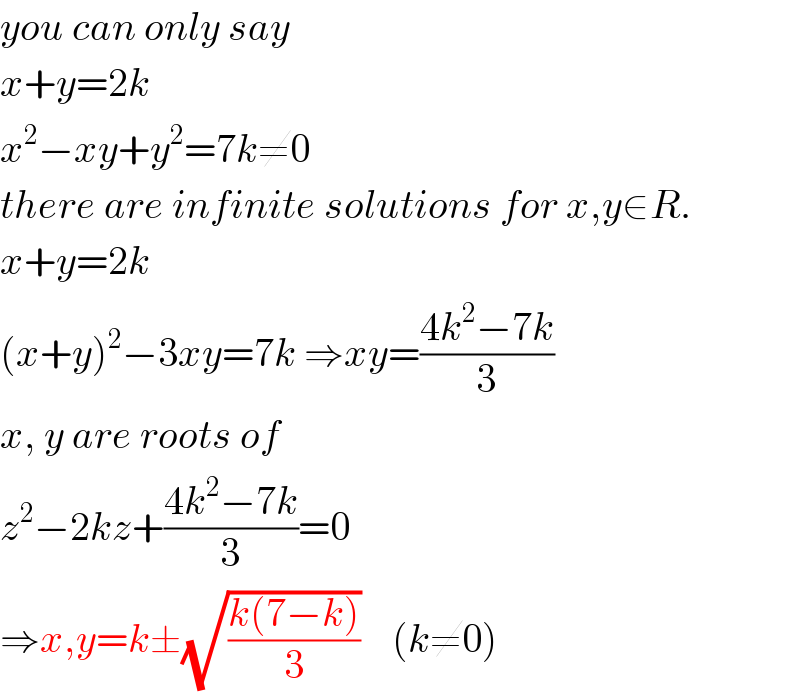
you can only say x+y=2k x^2 −xy+y^2 =7k≠0 there are infinite solutions for x,y∈R. x+y=2k (x+y)^2 −3xy=7k ⇒xy=((4k^2 −7k)/3) x, y are roots of z^2 −2kz+((4k^2 −7k)/3)=0 ⇒x,y=k±(√((k(7−k))/3)) (k≠0)
$${you}\:{can}\:{only}\:{say} \\ $$$${x}+{y}=\mathrm{2}{k} \\ $$$${x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} =\mathrm{7}{k}\neq\mathrm{0} \\ $$$${there}\:{are}\:{infinite}\:{solutions}\:{for}\:{x},{y}\in{R}. \\ $$$${x}+{y}=\mathrm{2}{k} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{3}{xy}=\mathrm{7}{k}\:\Rightarrow{xy}=\frac{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{7}{k}}{\mathrm{3}} \\ $$$${x},\:{y}\:{are}\:{roots}\:{of} \\ $$$${z}^{\mathrm{2}} −\mathrm{2}{kz}+\frac{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{7}{k}}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow{x},{y}={k}\pm\sqrt{\frac{{k}\left(\mathrm{7}−{k}\right)}{\mathrm{3}}}\:\:\:\:\left({k}\neq\mathrm{0}\right) \\ $$
Commented by mr W last updated on 25/Jun/20
((x+y)/(x^2 −xy+y^2 ))=(7/2) has also infinite solutions.
$$\frac{{x}+{y}}{{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$${has}\:{also}\:{infinite}\:{solutions}. \\ $$
Commented by Ar Brandon last updated on 25/Jun/20
I tried applying the same reasoning which you used above, but I get complex solutions √-123k²
Commented by Ar Brandon last updated on 25/Jun/20
Oh my ! I'm so very sorry. You're right, it's a mistake. It's supposed to be 7/2 . Thanks for the remark
Commented by Ar Brandon last updated on 25/Jun/20
Or perhabs I didn't do it in the right way.
Commented by mr W last updated on 25/Jun/20
x+y=7k x^2 −xy+y^2 =2k≠0 (x+y)^2 −3xy=2k ⇒xy=((49k^2 −2k)/3) z^2 −7kz+((49k^2 −2k)/3)=0 ⇒x, y=(1/2)[7k±(√((k(8−49k))/3))]
$${x}+{y}=\mathrm{7}{k} \\ $$$${x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} =\mathrm{2}{k}\neq\mathrm{0} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{3}{xy}=\mathrm{2}{k} \\ $$$$\Rightarrow{xy}=\frac{\mathrm{49}{k}^{\mathrm{2}} −\mathrm{2}{k}}{\mathrm{3}} \\ $$$${z}^{\mathrm{2}} −\mathrm{7}{kz}+\frac{\mathrm{49}{k}^{\mathrm{2}} −\mathrm{2}{k}}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow{x},\:{y}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{7}{k}\pm\sqrt{\frac{{k}\left(\mathrm{8}−\mathrm{49}{k}\right)}{\mathrm{3}}}\right] \\ $$
Commented by Ar Brandon last updated on 26/Jun/20
Thanks a lot for your time��
Answered by 4635 last updated on 26/Jun/20
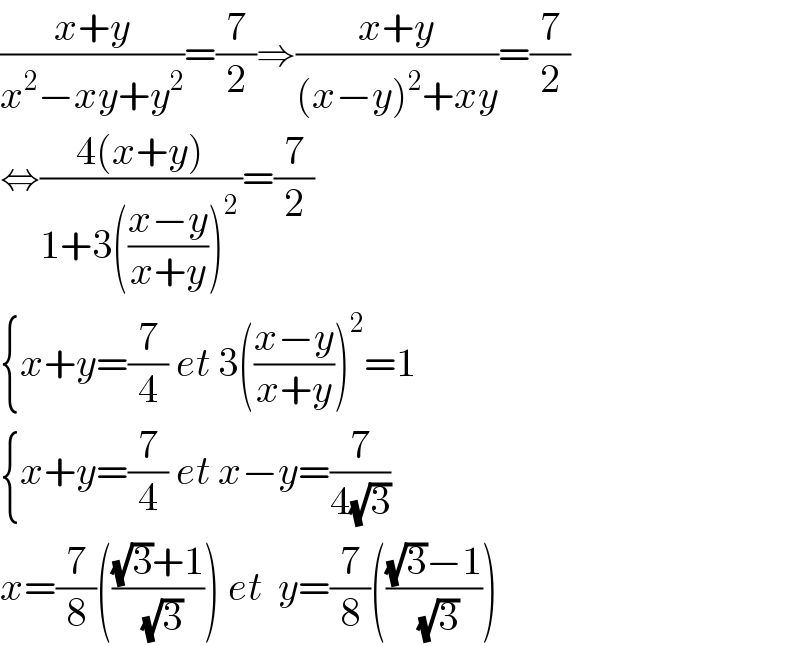
((x+y)/(x^2 −xy+y^2 ))=(7/2)⇒((x+y)/((x−y)^2 +xy))=(7/2) ⇔((4(x+y))/(1+3(((x−y)/(x+y)))^(2 ) ))=(7/2) {x+y=(7/4) et 3(((x−y)/(x+y)))^2 =1 {x+y=(7/4) et x−y=(7/(4(√3))) x=(7/8)((((√3)+1)/( (√3)))) et y=(7/8)((((√3)−1)/( (√3))))
$$\frac{{x}+{y}}{{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}}\Rightarrow\frac{{x}+{y}}{\left({x}−{y}\right)^{\mathrm{2}} +{xy}}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{\mathrm{4}\left({x}+{y}\right)}{\mathrm{1}+\mathrm{3}\left(\frac{{x}−{y}}{{x}+{y}}\right)^{\mathrm{2}\:} }=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\left\{{x}+{y}=\frac{\mathrm{7}}{\mathrm{4}}\:{et}\:\mathrm{3}\left(\frac{{x}−{y}}{{x}+{y}}\right)^{\mathrm{2}} =\mathrm{1}\right. \\ $$$$\left\{{x}+{y}=\frac{\mathrm{7}}{\mathrm{4}}\:{et}\:{x}−{y}=\frac{\mathrm{7}}{\mathrm{4}\sqrt{\mathrm{3}}}\right. \\ $$$${x}=\frac{\mathrm{7}}{\mathrm{8}}\left(\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:{et}\:\:{y}=\frac{\mathrm{7}}{\mathrm{8}}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$
Commented by mr W last updated on 26/Jun/20
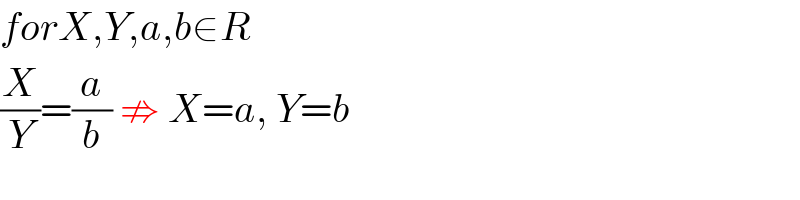
forX,Y,a,b∈R (X/Y)=(a/b) ⇏ X=a, Y=b
$${forX},{Y},{a},{b}\in{R} \\ $$$$\frac{{X}}{{Y}}=\frac{{a}}{{b}}\:\nRightarrow\:{X}={a},\:{Y}={b} \\ $$
Commented by Ar Brandon last updated on 26/Jun/20
Hum Takou, est-ce que tu as essayé de remplacer tes réponses dans l'équation pour voir si elles sont correctes ?��

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *