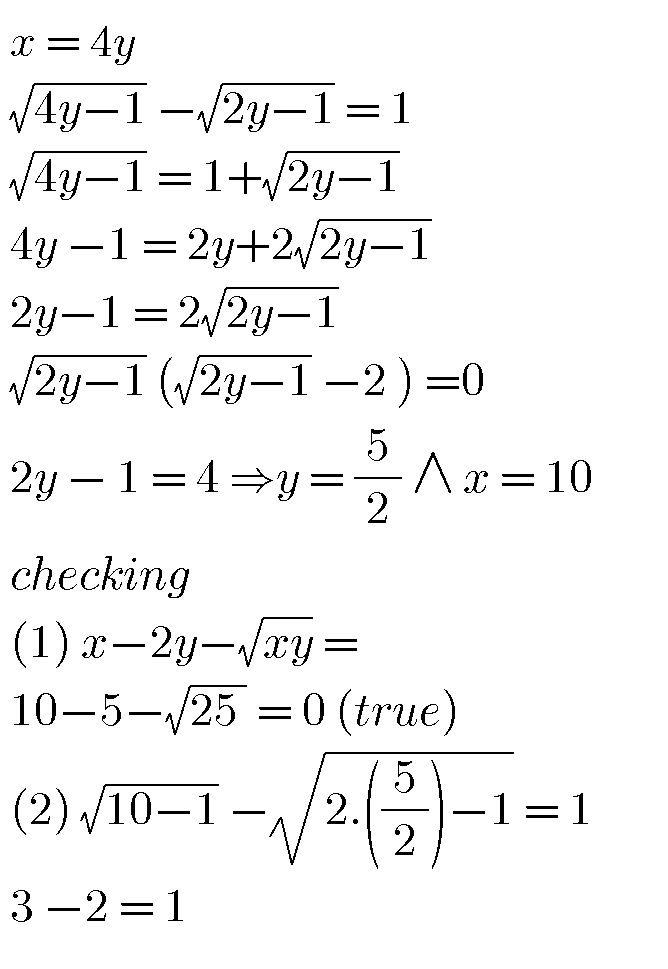find-x-y-x-2y-xy-0-x-1-2y-1-1-

Question Number 88921 by M±th+et£s last updated on 13/Apr/20

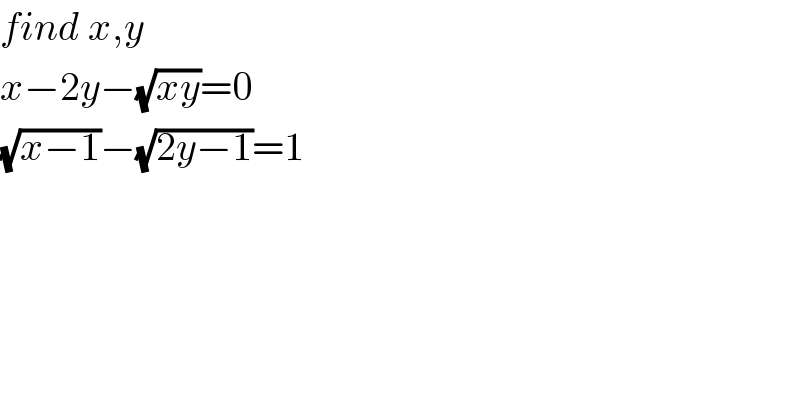
$${find}\:{x},{y} \\ $$$${x}−\mathrm{2}{y}−\sqrt{{xy}}=\mathrm{0} \\ $$$$\sqrt{{x}−\mathrm{1}}−\sqrt{\mathrm{2}{y}−\mathrm{1}}=\mathrm{1} \\ $$

Answered by behi83417@gmail.com last updated on 14/Apr/20

{ (((x−2y)^2 =xy⇒x^2 −4xy+4y^2 =xy)),(((√(x−1))−(√(2y−1))=1)) :} ⇒((x/y))+4((y/x))−5=0⇒(x/y)=1,4 1) x=y⇒(√(x−1))−(√(2y−1))=1 ⇒x−1−2(√(x−1))+1=2x−1 ⇒2(√(x−1))=1−x⇒4x−4=x^2 −2x+1 ⇒x^2 −6x+5=0⇒[x=y=1,5] 2)x=4y⇒4y−1−2(√(4y−1))+1=2y−1 ⇒2y+1=2(√(4y−1))⇒4y^2 +4y+1=16y−4 ⇒4y^2 −12y+5=0⇒y=((6±(√(36−20)))/4)=(5/2),(1/2) ⇒x=4y=10,2 thank you very much sir john. typo is fixed.

$$\begin{cases}{\left(\mathrm{x}−\mathrm{2y}\right)^{\mathrm{2}} =\mathrm{xy}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4xy}+\mathrm{4y}^{\mathrm{2}} =\mathrm{xy}}\\{\sqrt{\mathrm{x}−\mathrm{1}}−\sqrt{\mathrm{2y}−\mathrm{1}}=\mathrm{1}}\end{cases} \\ $$$$\Rightarrow\left(\frac{\mathrm{x}}{\mathrm{y}}\right)+\mathrm{4}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)−\mathrm{5}=\mathrm{0}\Rightarrow\frac{\mathrm{x}}{\mathrm{y}}=\mathrm{1},\mathrm{4} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{x}=\mathrm{y}\Rightarrow\sqrt{\mathrm{x}−\mathrm{1}}−\sqrt{\mathrm{2y}−\mathrm{1}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}−\mathrm{1}−\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}+\mathrm{1}=\mathrm{2x}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}=\mathrm{1}−\mathrm{x}\Rightarrow\mathrm{4x}−\mathrm{4}=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{5}=\mathrm{0}\Rightarrow\left[\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{y}}=\mathrm{1},\mathrm{5}\right] \\ $$$$\left.\mathrm{2}\right)\mathrm{x}=\mathrm{4y}\Rightarrow\mathrm{4y}−\mathrm{1}−\mathrm{2}\sqrt{\mathrm{4y}−\mathrm{1}}+\mathrm{1}=\mathrm{2y}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2y}+\mathrm{1}=\mathrm{2}\sqrt{\mathrm{4y}−\mathrm{1}}\Rightarrow\mathrm{4y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{1}=\mathrm{16y}−\mathrm{4} \\ $$$$\Rightarrow\mathrm{4y}^{\mathrm{2}} −\mathrm{12}\boldsymbol{\mathrm{y}}+\mathrm{5}=\mathrm{0}\Rightarrow\boldsymbol{\mathrm{y}}=\frac{\mathrm{6}\pm\sqrt{\mathrm{36}−\mathrm{20}}}{\mathrm{4}}=\frac{\mathrm{5}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{4y}=\mathrm{10},\mathrm{2} \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}\:\mathrm{john}. \\ $$$$\mathrm{typo}\:\mathrm{is}\:\mathrm{fixed}. \\ $$

Commented by M±th+et£s last updated on 14/Apr/20