Question Number 150531 by mathdanisur last updated on 13/Aug/21
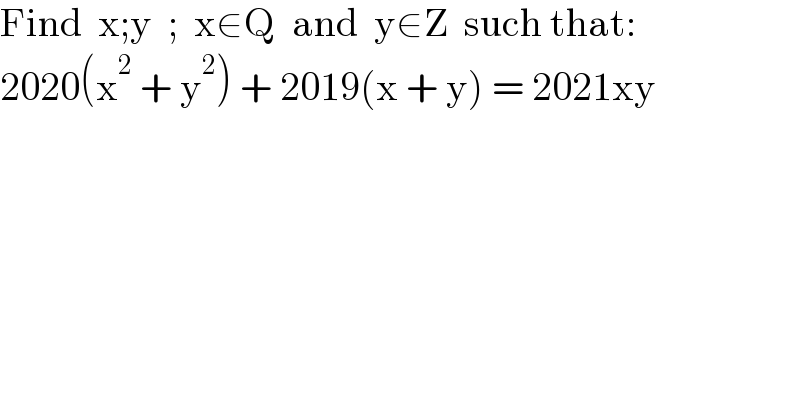
$$\mathrm{Find}\:\:\mathrm{x};\mathrm{y}\:\:;\:\:\mathrm{x}\in\mathrm{Q}\:\:\mathrm{and}\:\:\mathrm{y}\in\mathrm{Z}\:\:\mathrm{such}\:\mathrm{that}: \\ $$$$\mathrm{2020}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \right)\:+\:\mathrm{2019}\left(\mathrm{x}\:+\:\mathrm{y}\right)\:=\:\mathrm{2021xy} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Aug/21
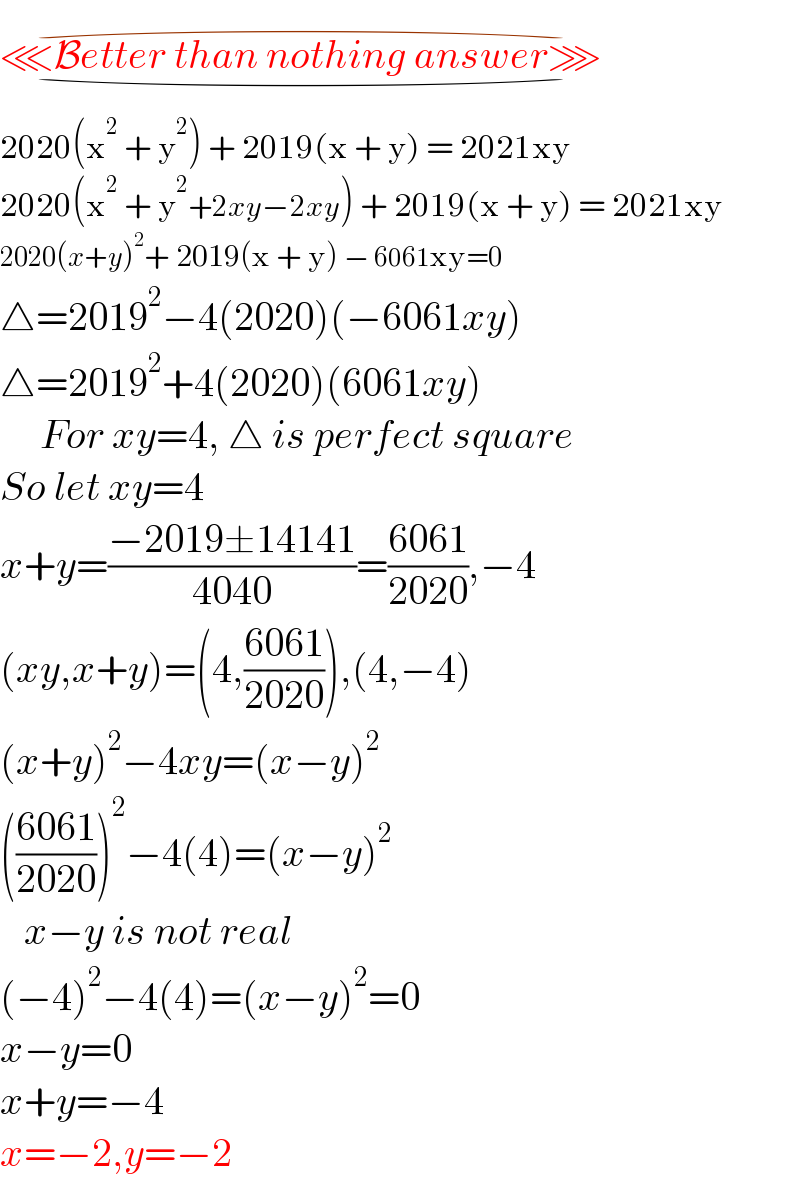
$$\underset{\smile} {\overset{\frown} {\lll\mathcal{B}{etter}\:{than}\:{nothing}\:{answer}\ggg}} \\ $$$$\mathrm{2020}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \right)\:+\:\mathrm{2019}\left(\mathrm{x}\:+\:\mathrm{y}\right)\:=\:\mathrm{2021xy} \\ $$$$\mathrm{2020}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} +\mathrm{2}{xy}−\mathrm{2}{xy}\right)\:+\:\mathrm{2019}\left(\mathrm{x}\:+\:\mathrm{y}\right)\:=\:\mathrm{2021xy} \\ $$$$\mathrm{2020}\left({x}+{y}\right)^{\mathrm{2}} +\:\mathrm{2019}\left(\mathrm{x}\:+\:\mathrm{y}\right)\:−\:\mathrm{6061xy}=\mathrm{0} \\ $$$$\bigtriangleup=\mathrm{2019}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{2020}\right)\left(−\mathrm{6061}{xy}\right) \\ $$$$\bigtriangleup=\mathrm{2019}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{2020}\right)\left(\mathrm{6061}{xy}\right) \\ $$$$\:\:\:\:\:{For}\:{xy}=\mathrm{4},\:\bigtriangleup\:{is}\:{perfect}\:{square} \\ $$$${So}\:{let}\:{xy}=\mathrm{4} \\ $$$${x}+{y}=\frac{−\mathrm{2019}\pm\mathrm{14141}}{\mathrm{4040}}=\frac{\mathrm{6061}}{\mathrm{2020}},−\mathrm{4} \\ $$$$\left({xy},{x}+{y}\right)=\left(\mathrm{4},\frac{\mathrm{6061}}{\mathrm{2020}}\right),\left(\mathrm{4},−\mathrm{4}\right) \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}=\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{6061}}{\mathrm{2020}}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{4}\right)=\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$\:\:\:{x}−{y}\:{is}\:{not}\:{real} \\ $$$$\left(−\mathrm{4}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{4}\right)=\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}−{y}=\mathrm{0} \\ $$$${x}+{y}=−\mathrm{4} \\ $$$${x}=−\mathrm{2},{y}=−\mathrm{2} \\ $$
Commented by mathdanisur last updated on 13/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser},\:\mathrm{but}\:\mathrm{ans}:\:\left(\mathrm{0};\mathrm{0}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 13/Aug/21
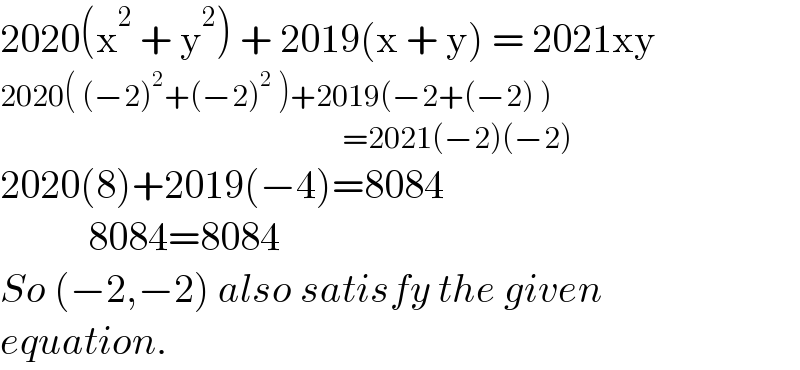
$$\mathrm{2020}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \right)\:+\:\mathrm{2019}\left(\mathrm{x}\:+\:\mathrm{y}\right)\:=\:\mathrm{2021xy} \\ $$$$\mathrm{2020}\left(\:\left(−\mathrm{2}\right)^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} \:\right)+\mathrm{2019}\left(−\mathrm{2}+\left(−\mathrm{2}\right)\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2021}\left(−\mathrm{2}\right)\left(−\mathrm{2}\right) \\ $$$$\mathrm{2020}\left(\mathrm{8}\right)+\mathrm{2019}\left(−\mathrm{4}\right)=\mathrm{8084} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{8084}=\mathrm{8084} \\ $$$${So}\:\left(−\mathrm{2},−\mathrm{2}\right)\:{also}\:{satisfy}\:{the}\:{given} \\ $$$${equation}. \\ $$
Commented by mathdanisur last updated on 13/Aug/21
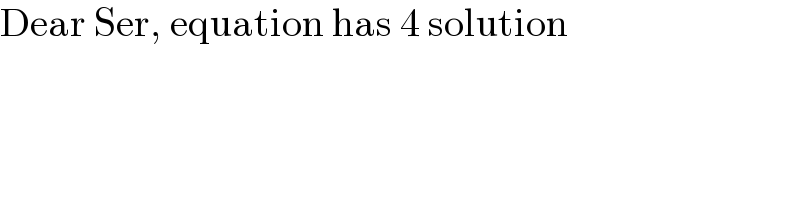
$$\mathrm{Dear}\:\mathrm{Ser},\:\mathrm{equation}\:\mathrm{has}\:\mathrm{4}\:\mathrm{solution} \\ $$
Commented by Rasheed.Sindhi last updated on 13/Aug/21
$${I}\:{didn}'{t}\:{say}\:{there}\:{is}\:{only}\:{this}\:{solution}, \\ $$$${I}\:{said}\:{this}\:{is}\:{also}\:{a}\:{solution}.{Thanks}. \\ $$$$ \\ $$
Commented by mathdanisur last updated on 14/Aug/21

$$\mathrm{Thankyou}\:\mathrm{Ser} \\ $$
