Question Number 156452 by MathSh last updated on 11/Oct/21
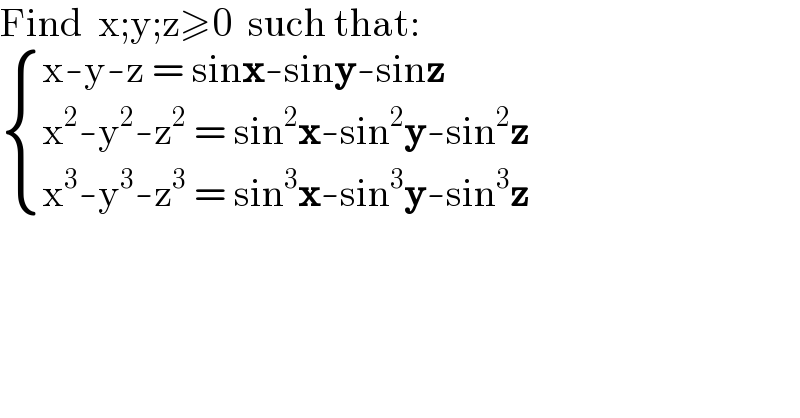
$$\mathrm{Find}\:\:\mathrm{x};\mathrm{y};\mathrm{z}\geqslant\mathrm{0}\:\:\mathrm{such}\:\mathrm{that}: \\ $$$$\begin{cases}{\mathrm{x}-\mathrm{y}-\mathrm{z}\:=\:\mathrm{sin}\boldsymbol{\mathrm{x}}-\mathrm{sin}\boldsymbol{\mathrm{y}}-\mathrm{sin}\boldsymbol{\mathrm{z}}}\\{\mathrm{x}^{\mathrm{2}} -\mathrm{y}^{\mathrm{2}} -\mathrm{z}^{\mathrm{2}} \:=\:\mathrm{sin}^{\mathrm{2}} \boldsymbol{\mathrm{x}}-\mathrm{sin}^{\mathrm{2}} \boldsymbol{\mathrm{y}}-\mathrm{sin}^{\mathrm{2}} \boldsymbol{\mathrm{z}}}\\{\mathrm{x}^{\mathrm{3}} -\mathrm{y}^{\mathrm{3}} -\mathrm{z}^{\mathrm{3}} \:=\:\mathrm{sin}^{\mathrm{3}} \boldsymbol{\mathrm{x}}-\mathrm{sin}^{\mathrm{3}} \boldsymbol{\mathrm{y}}-\mathrm{sin}^{\mathrm{3}} \boldsymbol{\mathrm{z}}}\end{cases} \\ $$
