Question Number 101271 by mathmax by abdo last updated on 01/Jul/20
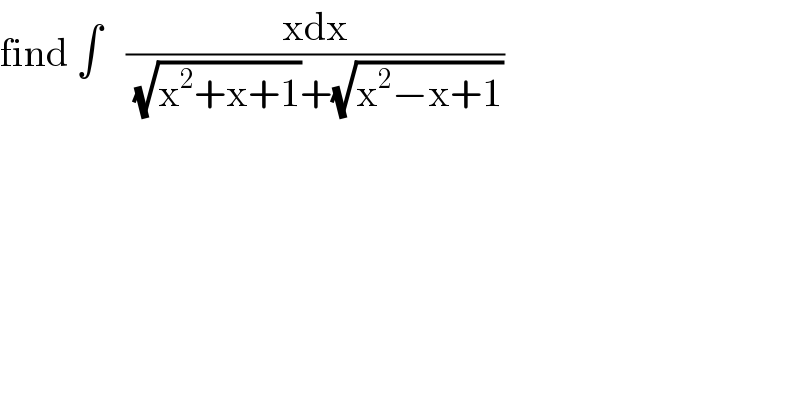
$$\mathrm{find}\:\int\:\:\:\frac{\mathrm{xdx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20
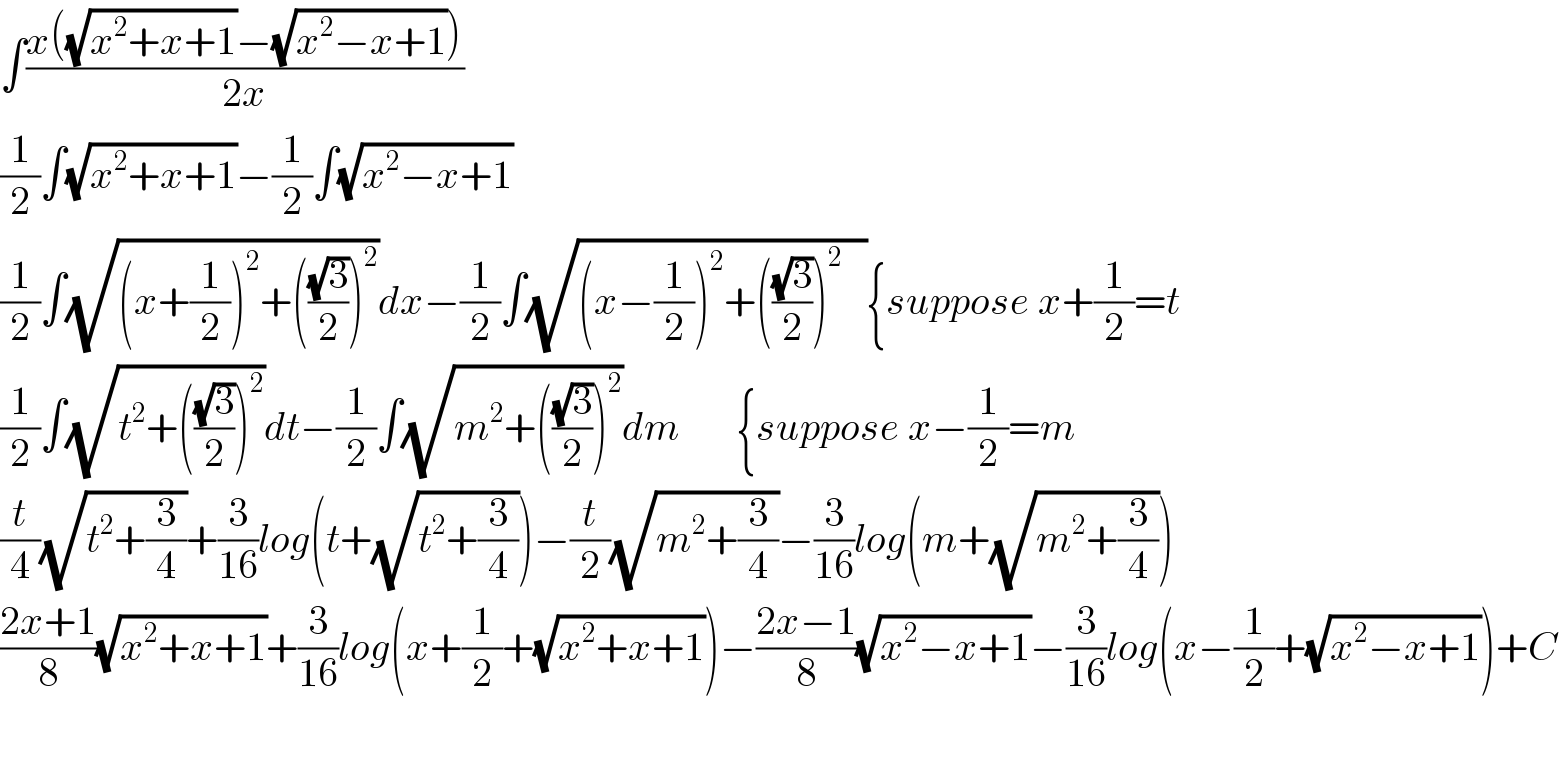
$$\int\frac{{x}\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\right)}{\mathrm{2}{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\:}\left\{{suppose}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}={t}\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{t}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{m}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{dm}\:\:\:\:\:\:\:\left\{{suppose}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}={m}\right. \\ $$$$\frac{{t}}{\mathrm{4}}\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}+\frac{\mathrm{3}}{\mathrm{16}}{log}\left({t}+\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\right)−\frac{{t}}{\mathrm{2}}\sqrt{{m}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}−\frac{\mathrm{3}}{\mathrm{16}}{log}\left({m}+\sqrt{{m}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\right) \\ $$$$\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{8}}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{16}}{log}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)−\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{8}}\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{16}}{log}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\right)+{C} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 02/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
