Question Number 172013 by Mikenice last updated on 23/Jun/22

$${find}: \\ $$$$\int{xe}^{−{ax}} {ax} \\ $$
Answered by puissant last updated on 23/Jun/22
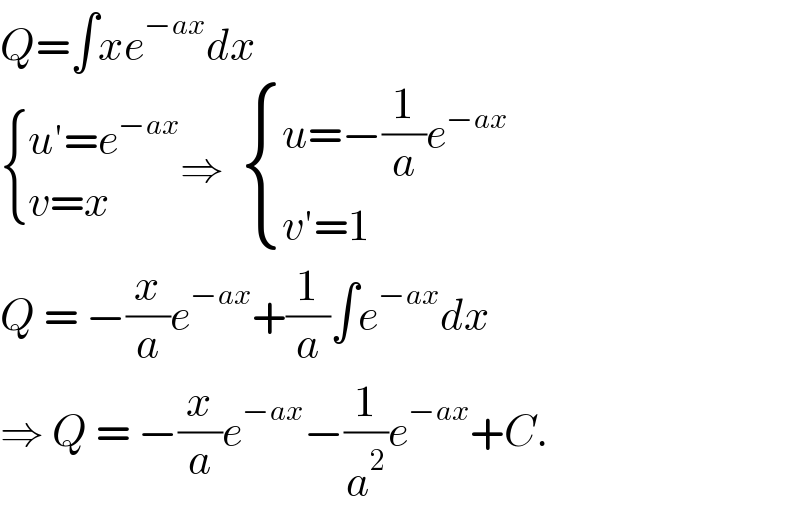
$${Q}=\int{xe}^{−{ax}} {dx}\:\: \\ $$$$\begin{cases}{{u}'={e}^{−{ax}} }\\{{v}={x}\:\:}\end{cases}\Rightarrow\:\:\begin{cases}{{u}=−\frac{\mathrm{1}}{{a}}{e}^{−{ax}} }\\{{v}'=\mathrm{1}}\end{cases} \\ $$$${Q}\:=\:−\frac{{x}}{{a}}{e}^{−{ax}} +\frac{\mathrm{1}}{{a}}\int{e}^{−{ax}} {dx} \\ $$$$\Rightarrow\:{Q}\:=\:−\frac{{x}}{{a}}{e}^{−{ax}} −\frac{\mathrm{1}}{{a}^{\mathrm{2}} }{e}^{−{ax}} +{C}. \\ $$
