Menu Close

find-z-1-3-cos-piz-z-2-z-2-4-dz-

Tinku Tara 0 Comments
Pin




Question Number 146546 by mathmax by abdo last updated on 13/Jul/21
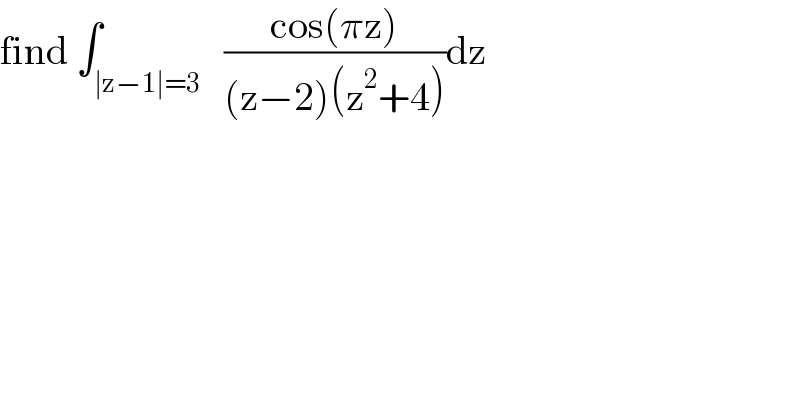
find ∫_(∣z−1∣=3) ((cos(πz))/((z−2)(z^2 +4)))dz
$$\mathrm{find}\:\int_{\mid\mathrm{z}−\mathrm{1}\mid=\mathrm{3}} \:\:\frac{\mathrm{cos}\left(\pi\mathrm{z}\right)}{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)}\mathrm{dz} \\ $$
Answered by Olaf_Thorendsen last updated on 14/Jul/21
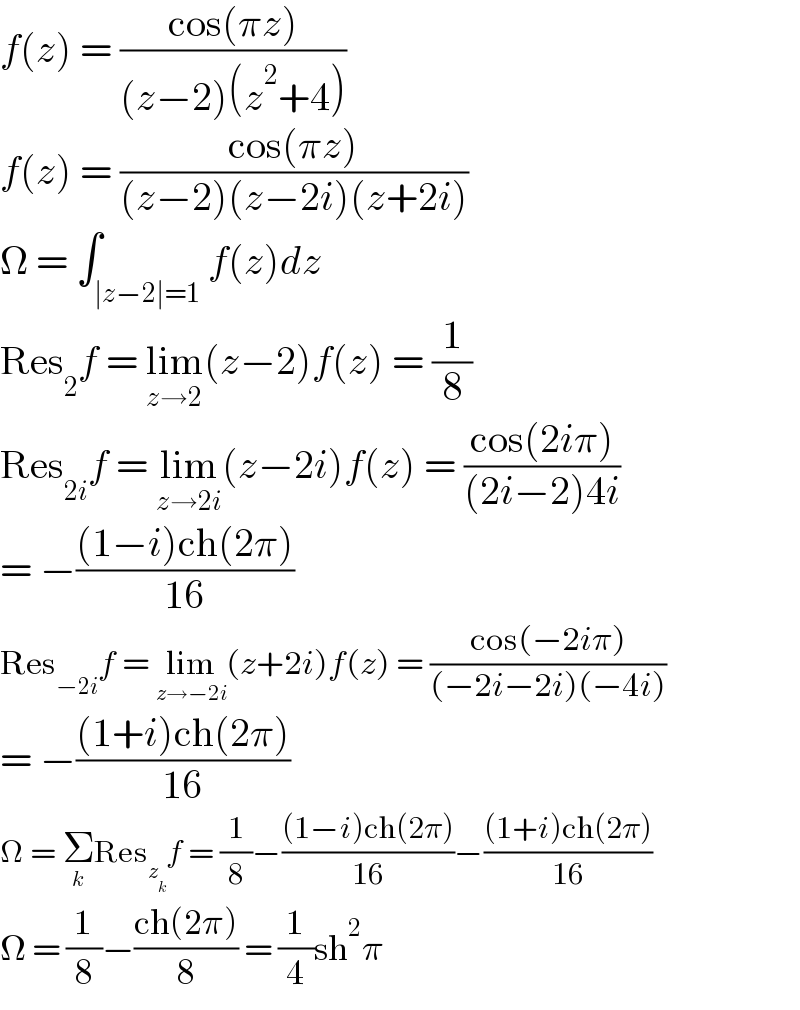
f(z) = ((cos(πz))/((z−2)(z^2 +4))) f(z) = ((cos(πz))/((z−2)(z−2i)(z+2i))) Ω = ∫_(∣z−2∣=1) f(z)dz Res_2 f = lim_(z→2) (z−2)f(z) = (1/8) Res_(2i) f = lim_(z→2i) (z−2i)f(z) = ((cos(2iπ))/((2i−2)4i)) = −(((1−i)ch(2π))/(16)) Res_(−2i) f = lim_(z→−2i) (z+2i)f(z) = ((cos(−2iπ))/((−2i−2i)(−4i))) = −(((1+i)ch(2π))/(16)) Ω = Σ_k Res_z_k f = (1/8)−(((1−i)ch(2π))/(16))−(((1+i)ch(2π))/(16)) Ω = (1/8)−((ch(2π))/8) = (1/4)sh^2 π
$${f}\left({z}\right)\:=\:\frac{\mathrm{cos}\left(\pi{z}\right)}{\left({z}−\mathrm{2}\right)\left({z}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{cos}\left(\pi{z}\right)}{\left({z}−\mathrm{2}\right)\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)} \\ $$$$\Omega\:=\:\int_{\mid{z}−\mathrm{2}\mid=\mathrm{1}} {f}\left({z}\right){dz} \\ $$$$\mathrm{Res}_{\mathrm{2}} {f}\:=\:\underset{{z}\rightarrow\mathrm{2}} {\mathrm{lim}}\left({z}−\mathrm{2}\right){f}\left({z}\right)\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{Res}_{\mathrm{2}{i}} {f}\:=\:\underset{{z}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\left({z}−\mathrm{2}{i}\right){f}\left({z}\right)\:=\:\frac{\mathrm{cos}\left(\mathrm{2}{i}\pi\right)}{\left(\mathrm{2}{i}−\mathrm{2}\right)\mathrm{4}{i}} \\ $$$$=\:−\frac{\left(\mathrm{1}−{i}\right)\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{16}} \\ $$$$\mathrm{Res}_{−\mathrm{2}{i}} {f}\:=\:\underset{{z}\rightarrow−\mathrm{2}{i}} {\mathrm{lim}}\left({z}+\mathrm{2}{i}\right){f}\left({z}\right)\:=\:\frac{\mathrm{cos}\left(−\mathrm{2}{i}\pi\right)}{\left(−\mathrm{2}{i}−\mathrm{2}{i}\right)\left(−\mathrm{4}{i}\right)} \\ $$$$=\:−\frac{\left(\mathrm{1}+{i}\right)\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{16}} \\ $$$$\Omega\:=\:\underset{{k}} {\sum}\mathrm{Res}_{{z}_{{k}} } {f}\:=\:\frac{\mathrm{1}}{\mathrm{8}}−\frac{\left(\mathrm{1}−{i}\right)\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{16}}−\frac{\left(\mathrm{1}+{i}\right)\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{16}} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{8}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sh}^{\mathrm{2}} \pi \\ $$
Answered by mathmax by abdo last updated on 14/Jul/21
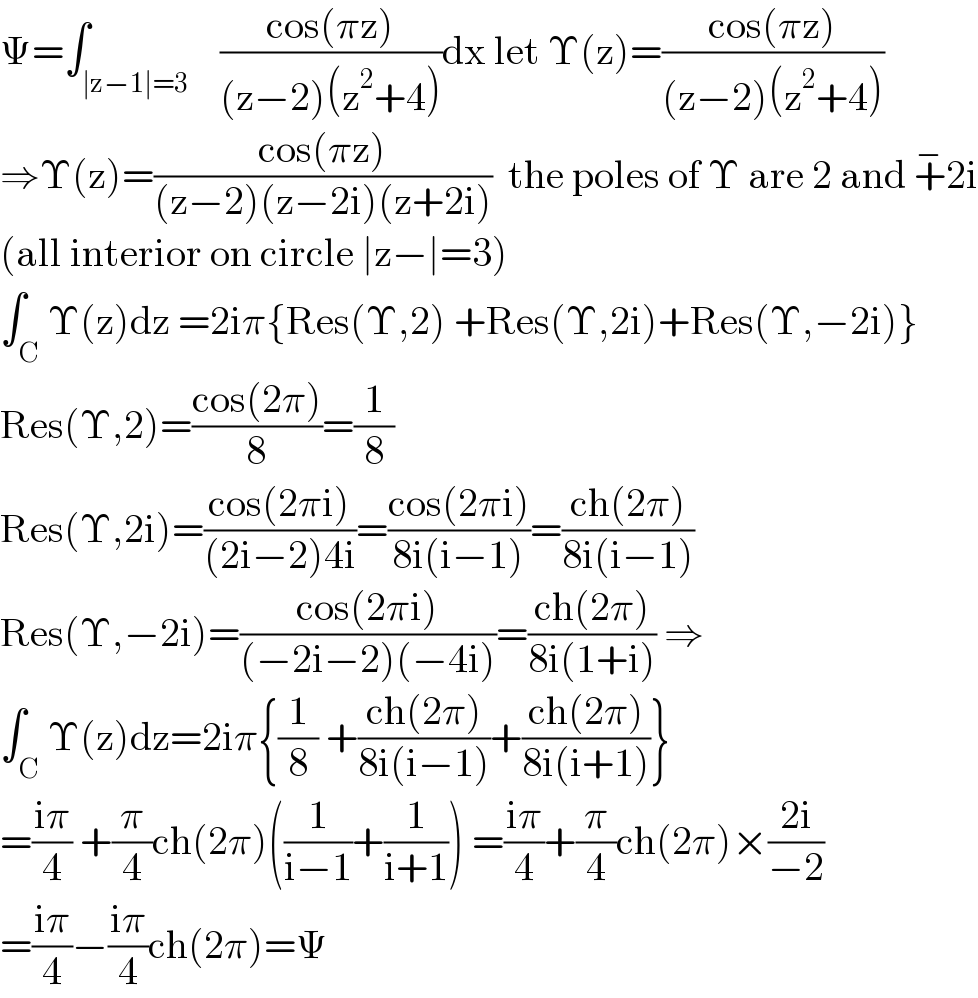
Ψ=∫_(∣z−1∣=3) ((cos(πz))/((z−2)(z^2 +4)))dx let Υ(z)=((cos(πz))/((z−2)(z^2 +4))) ⇒Υ(z)=((cos(πz))/((z−2)(z−2i)(z+2i))) the poles of Υ are 2 and +^− 2i (all interior on circle ∣z−∣=3) ∫_C Υ(z)dz =2iπ{Res(Υ,2) +Res(Υ,2i)+Res(Υ,−2i)} Res(Υ,2)=((cos(2π))/8)=(1/8) Res(Υ,2i)=((cos(2πi))/((2i−2)4i))=((cos(2πi))/(8i(i−1)))=((ch(2π))/(8i(i−1))) Res(Υ,−2i)=((cos(2πi))/((−2i−2)(−4i)))=((ch(2π))/(8i(1+i))) ⇒ ∫_C Υ(z)dz=2iπ{(1/8) +((ch(2π))/(8i(i−1)))+((ch(2π))/(8i(i+1)))} =((iπ)/4) +(π/4)ch(2π)((1/(i−1))+(1/(i+1))) =((iπ)/4)+(π/4)ch(2π)×((2i)/(−2)) =((iπ)/4)−((iπ)/4)ch(2π)=Ψ
$$\Psi=\int_{\mid\mathrm{z}−\mathrm{1}\mid=\mathrm{3}} \:\:\:\frac{\mathrm{cos}\left(\pi\mathrm{z}\right)}{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)}\mathrm{dx}\:\mathrm{let}\:\Upsilon\left(\mathrm{z}\right)=\frac{\mathrm{cos}\left(\pi\mathrm{z}\right)}{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$$$\Rightarrow\Upsilon\left(\mathrm{z}\right)=\frac{\mathrm{cos}\left(\pi\mathrm{z}\right)}{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}−\mathrm{2i}\right)\left(\mathrm{z}+\mathrm{2i}\right)}\:\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\Upsilon\:\mathrm{are}\:\mathrm{2}\:\mathrm{and}\:\overset{−} {+}\mathrm{2i} \\ $$$$\left(\mathrm{all}\:\mathrm{interior}\:\mathrm{on}\:\mathrm{circle}\:\mid\mathrm{z}−\mid=\mathrm{3}\right) \\ $$$$\int_{\mathrm{C}} \Upsilon\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\Upsilon,\mathrm{2}\right)\:+\mathrm{Res}\left(\Upsilon,\mathrm{2i}\right)+\mathrm{Res}\left(\Upsilon,−\mathrm{2i}\right)\right\} \\ $$$$\mathrm{Res}\left(\Upsilon,\mathrm{2}\right)=\frac{\mathrm{cos}\left(\mathrm{2}\pi\right)}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{Res}\left(\Upsilon,\mathrm{2i}\right)=\frac{\mathrm{cos}\left(\mathrm{2}\pi\mathrm{i}\right)}{\left(\mathrm{2i}−\mathrm{2}\right)\mathrm{4i}}=\frac{\mathrm{cos}\left(\mathrm{2}\pi\mathrm{i}\right)}{\mathrm{8i}\left(\mathrm{i}−\mathrm{1}\right)}=\frac{\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{8i}\left(\mathrm{i}−\mathrm{1}\right)} \\ $$$$\mathrm{Res}\left(\Upsilon,−\mathrm{2i}\right)=\frac{\mathrm{cos}\left(\mathrm{2}\pi\mathrm{i}\right)}{\left(−\mathrm{2i}−\mathrm{2}\right)\left(−\mathrm{4i}\right)}=\frac{\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{8i}\left(\mathrm{1}+\mathrm{i}\right)}\:\Rightarrow \\ $$$$\int_{\mathrm{C}} \Upsilon\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\left\{\frac{\mathrm{1}}{\mathrm{8}}\:+\frac{\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{8i}\left(\mathrm{i}−\mathrm{1}\right)}+\frac{\mathrm{ch}\left(\mathrm{2}\pi\right)}{\mathrm{8i}\left(\mathrm{i}+\mathrm{1}\right)}\right\} \\ $$$$=\frac{\mathrm{i}\pi}{\mathrm{4}}\:+\frac{\pi}{\mathrm{4}}\mathrm{ch}\left(\mathrm{2}\pi\right)\left(\frac{\mathrm{1}}{\mathrm{i}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{i}+\mathrm{1}}\right)\:=\frac{\mathrm{i}\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}\mathrm{ch}\left(\mathrm{2}\pi\right)×\frac{\mathrm{2i}}{−\mathrm{2}} \\ $$$$=\frac{\mathrm{i}\pi}{\mathrm{4}}−\frac{\mathrm{i}\pi}{\mathrm{4}}\mathrm{ch}\left(\mathrm{2}\pi\right)=\Psi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *