Question Number 56192 by 121194 last updated on 11/Mar/19
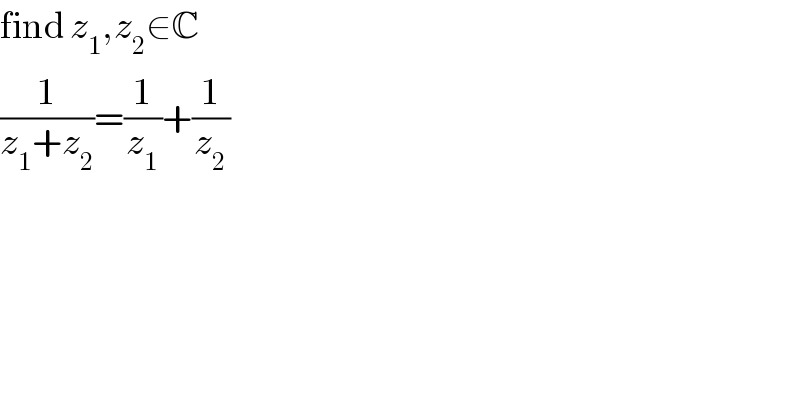
$$\mathrm{find}\:{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} \in\mathbb{C} \\ $$$$\frac{\mathrm{1}}{{z}_{\mathrm{1}} +{z}_{\mathrm{2}} }=\frac{\mathrm{1}}{{z}_{\mathrm{1}} }+\frac{\mathrm{1}}{{z}_{\mathrm{2}} } \\ $$
Answered by MJS last updated on 11/Mar/19
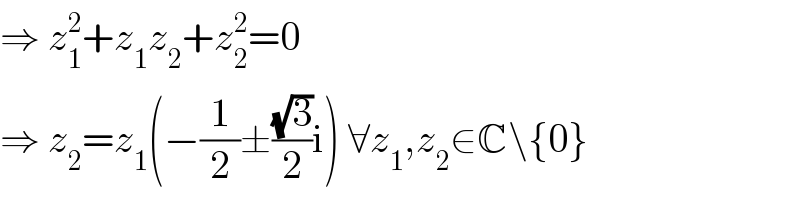
$$\Rightarrow\:{z}_{\mathrm{1}} ^{\mathrm{2}} +{z}_{\mathrm{1}} {z}_{\mathrm{2}} +{z}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:{z}_{\mathrm{2}} ={z}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\:\forall{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} \in\mathbb{C}\backslash\left\{\mathrm{0}\right\} \\ $$
