Menu Close

fog-6x-2-2x-3-gof-12x-2-14x-6-f-2-

Tinku Tara 0 Comments
Pin




Question Number 165021 by mathlove last updated on 25/Jan/22
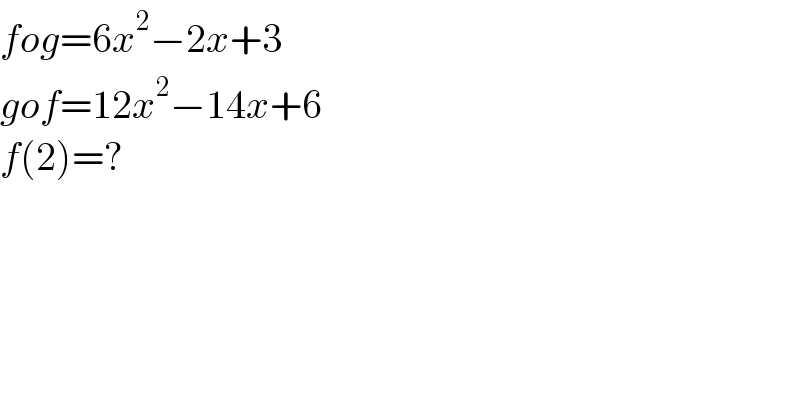
fog=6x^2 −2x+3 gof=12x^2 −14x+6 f(2)=?
$${fog}=\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3} \\ $$$${gof}=\mathrm{12}{x}^{\mathrm{2}} −\mathrm{14}{x}+\mathrm{6} \\ $$$${f}\left(\mathrm{2}\right)=? \\ $$
Answered by mr W last updated on 25/Jan/22
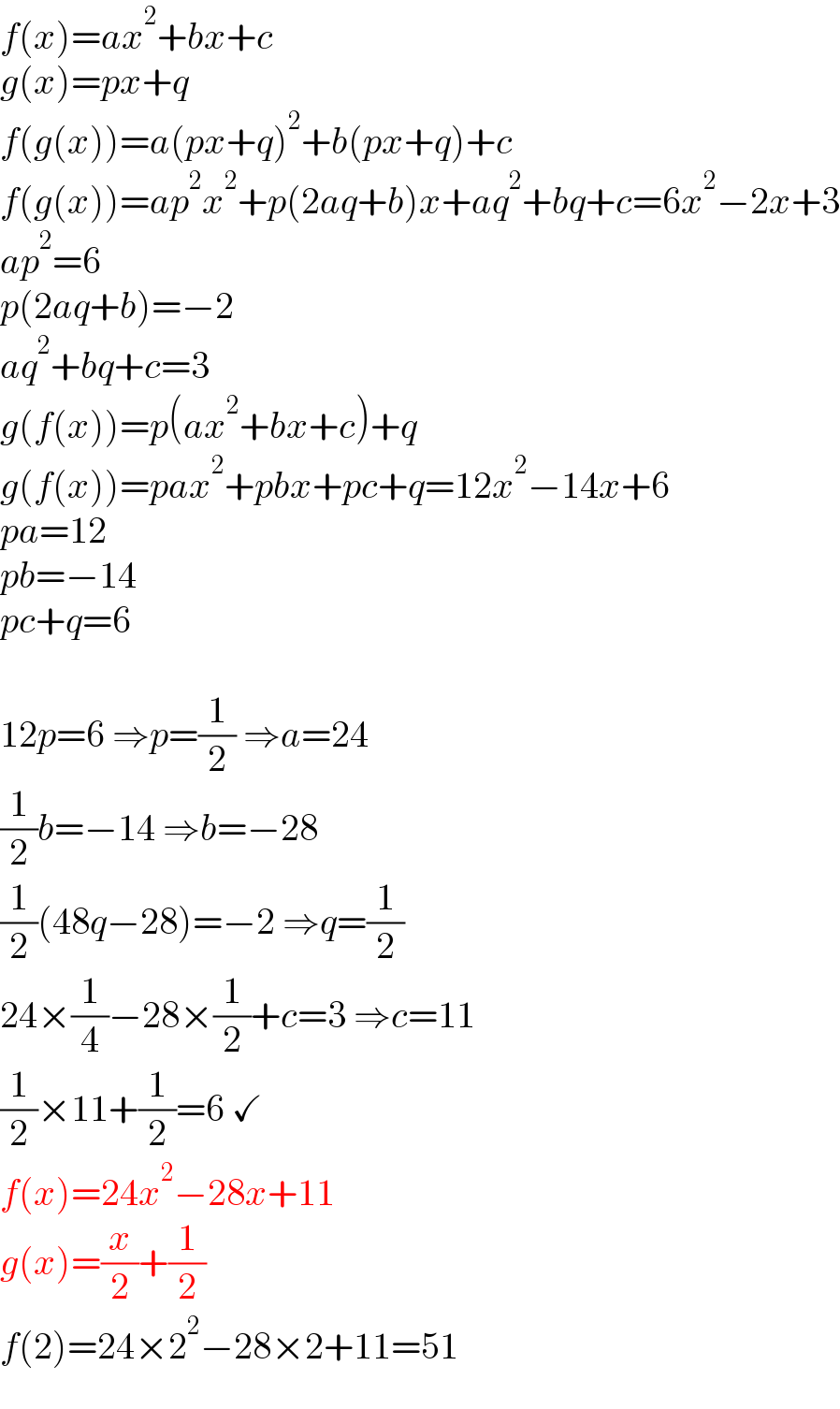
f(x)=ax^2 +bx+c g(x)=px+q f(g(x))=a(px+q)^2 +b(px+q)+c f(g(x))=ap^2 x^2 +p(2aq+b)x+aq^2 +bq+c=6x^2 −2x+3 ap^2 =6 p(2aq+b)=−2 aq^2 +bq+c=3 g(f(x))=p(ax^2 +bx+c)+q g(f(x))=pax^2 +pbx+pc+q=12x^2 −14x+6 pa=12 pb=−14 pc+q=6 12p=6 ⇒p=(1/2) ⇒a=24 (1/2)b=−14 ⇒b=−28 (1/2)(48q−28)=−2 ⇒q=(1/2) 24×(1/4)−28×(1/2)+c=3 ⇒c=11 (1/2)×11+(1/2)=6 ✓ f(x)=24x^2 −28x+11 g(x)=(x/2)+(1/2) f(2)=24×2^2 −28×2+11=51
$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${g}\left({x}\right)={px}+{q} \\ $$$${f}\left({g}\left({x}\right)\right)={a}\left({px}+{q}\right)^{\mathrm{2}} +{b}\left({px}+{q}\right)+{c} \\ $$$${f}\left({g}\left({x}\right)\right)={ap}^{\mathrm{2}} {x}^{\mathrm{2}} +{p}\left(\mathrm{2}{aq}+{b}\right){x}+{aq}^{\mathrm{2}} +{bq}+{c}=\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3} \\ $$$${ap}^{\mathrm{2}} =\mathrm{6} \\ $$$${p}\left(\mathrm{2}{aq}+{b}\right)=−\mathrm{2} \\ $$$${aq}^{\mathrm{2}} +{bq}+{c}=\mathrm{3} \\ $$$${g}\left({f}\left({x}\right)\right)={p}\left({ax}^{\mathrm{2}} +{bx}+{c}\right)+{q} \\ $$$${g}\left({f}\left({x}\right)\right)={pax}^{\mathrm{2}} +{pbx}+{pc}+{q}=\mathrm{12}{x}^{\mathrm{2}} −\mathrm{14}{x}+\mathrm{6} \\ $$$${pa}=\mathrm{12} \\ $$$${pb}=−\mathrm{14} \\ $$$${pc}+{q}=\mathrm{6} \\ $$$$ \\ $$$$\mathrm{12}{p}=\mathrm{6}\:\Rightarrow{p}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{a}=\mathrm{24} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{b}=−\mathrm{14}\:\Rightarrow{b}=−\mathrm{28} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{48}{q}−\mathrm{28}\right)=−\mathrm{2}\:\Rightarrow{q}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{24}×\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{28}×\frac{\mathrm{1}}{\mathrm{2}}+{c}=\mathrm{3}\:\Rightarrow{c}=\mathrm{11} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{11}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{6}\:\checkmark \\ $$$${f}\left({x}\right)=\mathrm{24}{x}^{\mathrm{2}} −\mathrm{28}{x}+\mathrm{11} \\ $$$${g}\left({x}\right)=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{24}×\mathrm{2}^{\mathrm{2}} −\mathrm{28}×\mathrm{2}+\mathrm{11}=\mathrm{51} \\ $$
Commented by aleks041103 last updated on 25/Jan/22
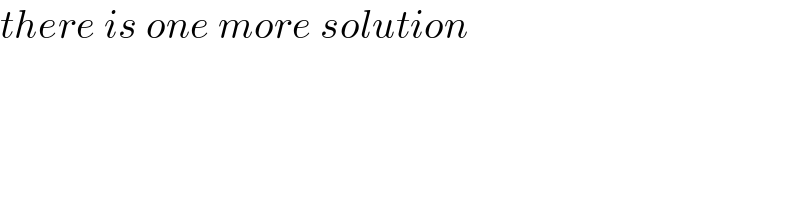
there is one more solution
$${there}\:{is}\:{one}\:{more}\:{solution} \\ $$
Commented by mr W last updated on 25/Jan/22
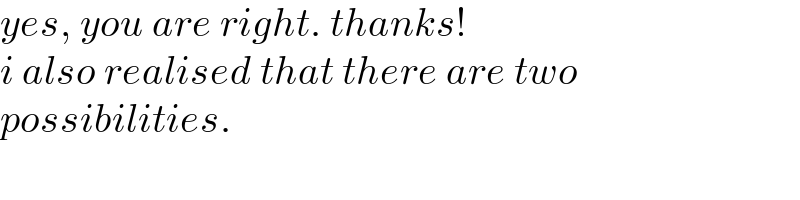
yes, you are right. thanks! i also realised that there are two possibilities.
$${yes},\:{you}\:{are}\:{right}.\:{thanks}! \\ $$$${i}\:{also}\:{realised}\:{that}\:{there}\:{are}\:{two}\: \\ $$$${possibilities}. \\ $$
Commented by Tawa11 last updated on 25/Jan/22
Weldone sirs
$$\mathrm{Weldone}\:\mathrm{sirs} \\ $$
Answered by aleks041103 last updated on 25/Jan/22
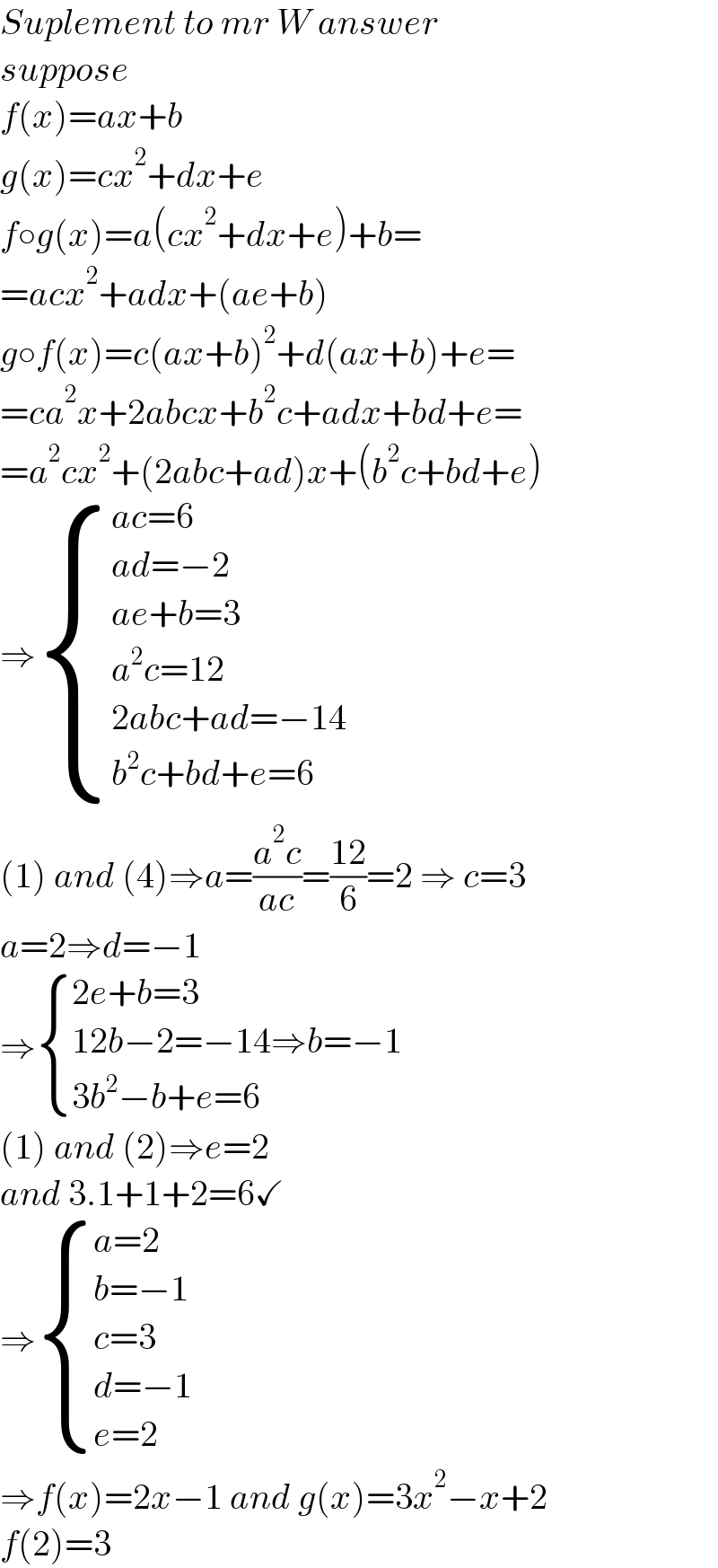
Suplement to mr W answer suppose f(x)=ax+b g(x)=cx^2 +dx+e f○g(x)=a(cx^2 +dx+e)+b= =acx^2 +adx+(ae+b) g○f(x)=c(ax+b)^2 +d(ax+b)+e= =ca^2 x+2abcx+b^2 c+adx+bd+e= =a^2 cx^2 +(2abc+ad)x+(b^2 c+bd+e) ⇒ { ((ac=6)),((ad=−2)),((ae+b=3)),((a^2 c=12)),((2abc+ad=−14)),((b^2 c+bd+e=6)) :} (1) and (4)⇒a=((a^2 c)/(ac))=((12)/6)=2 ⇒ c=3 a=2⇒d=−1 ⇒ { ((2e+b=3)),((12b−2=−14⇒b=−1)),((3b^2 −b+e=6)) :} (1) and (2)⇒e=2 and 3.1+1+2=6✓ ⇒ { ((a=2)),((b=−1)),((c=3)),((d=−1)),((e=2)) :} ⇒f(x)=2x−1 and g(x)=3x^2 −x+2 f(2)=3
$${Suplement}\:{to}\:{mr}\:{W}\:{answer} \\ $$$${suppose} \\ $$$${f}\left({x}\right)={ax}+{b} \\ $$$${g}\left({x}\right)={cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${f}\circ{g}\left({x}\right)={a}\left({cx}^{\mathrm{2}} +{dx}+{e}\right)+{b}= \\ $$$$={acx}^{\mathrm{2}} +{adx}+\left({ae}+{b}\right) \\ $$$${g}\circ{f}\left({x}\right)={c}\left({ax}+{b}\right)^{\mathrm{2}} +{d}\left({ax}+{b}\right)+{e}= \\ $$$$={ca}^{\mathrm{2}} {x}+\mathrm{2}{abcx}+{b}^{\mathrm{2}} {c}+{adx}+{bd}+{e}= \\ $$$$={a}^{\mathrm{2}} {cx}^{\mathrm{2}} +\left(\mathrm{2}{abc}+{ad}\right){x}+\left({b}^{\mathrm{2}} {c}+{bd}+{e}\right) \\ $$$$\Rightarrow\begin{cases}{{ac}=\mathrm{6}}\\{{ad}=−\mathrm{2}}\\{{ae}+{b}=\mathrm{3}}\\{{a}^{\mathrm{2}} {c}=\mathrm{12}}\\{\mathrm{2}{abc}+{ad}=−\mathrm{14}}\\{{b}^{\mathrm{2}} {c}+{bd}+{e}=\mathrm{6}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{4}\right)\Rightarrow{a}=\frac{{a}^{\mathrm{2}} {c}}{{ac}}=\frac{\mathrm{12}}{\mathrm{6}}=\mathrm{2}\:\Rightarrow\:{c}=\mathrm{3} \\ $$$${a}=\mathrm{2}\Rightarrow{d}=−\mathrm{1} \\ $$$$\Rightarrow\begin{cases}{\mathrm{2}{e}+{b}=\mathrm{3}}\\{\mathrm{12}{b}−\mathrm{2}=−\mathrm{14}\Rightarrow{b}=−\mathrm{1}}\\{\mathrm{3}{b}^{\mathrm{2}} −{b}+{e}=\mathrm{6}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right)\Rightarrow{e}=\mathrm{2} \\ $$$${and}\:\mathrm{3}.\mathrm{1}+\mathrm{1}+\mathrm{2}=\mathrm{6}\checkmark \\ $$$$\Rightarrow\begin{cases}{{a}=\mathrm{2}}\\{{b}=−\mathrm{1}}\\{{c}=\mathrm{3}}\\{{d}=−\mathrm{1}}\\{{e}=\mathrm{2}}\end{cases} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}{x}−\mathrm{1}\:{and}\:{g}\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} −{x}+\mathrm{2} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *