Question Number 81598 by zainal tanjung last updated on 03/Mar/20

$$\mathrm{fog}\left(\mathrm{x}\right)=\mathrm{8x}+\mathrm{3} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=…..? \\ $$$$ \\ $$$$\mathrm{gof}\left(\mathrm{x}\right)=\mathrm{6x}+\mathrm{1} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{5x}+\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=…..? \\ $$$$ \\ $$$$\mathrm{gof}\left(\mathrm{x}\right)=\mathrm{7x}+\mathrm{9} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{5x}+\mathrm{2} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=…..? \\ $$$$ \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3x}−\mathrm{8} \\ $$$$\mathrm{gof}\left(\mathrm{x}\right)=\mathrm{8x}+\mathrm{3} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=…..? \\ $$$$ \\ $$$$\mathrm{gof}\left(\mathrm{x}\right)=\mathrm{5x}+\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3x} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=….? \\ $$$$ \\ $$
Commented by Tony Lin last updated on 14/Feb/20
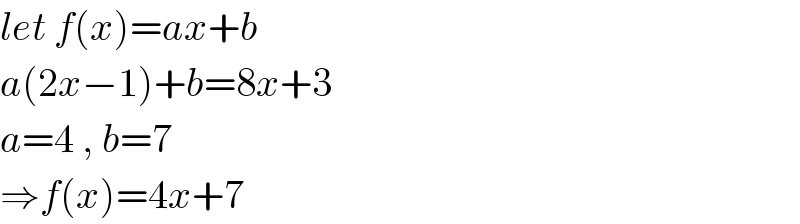
$${let}\:{f}\left({x}\right)={ax}+{b} \\ $$$${a}\left(\mathrm{2}{x}−\mathrm{1}\right)+{b}=\mathrm{8}{x}+\mathrm{3} \\ $$$${a}=\mathrm{4}\:,\:{b}=\mathrm{7} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{4}{x}+\mathrm{7} \\ $$
Commented by mr W last updated on 14/Feb/20
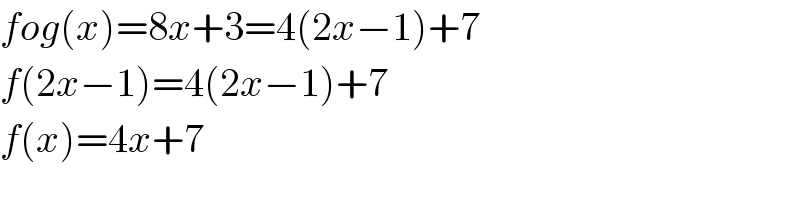
$${fog}\left({x}\right)=\mathrm{8}{x}+\mathrm{3}=\mathrm{4}\left(\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{7} \\ $$$${f}\left(\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{4}\left(\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{7} \\ $$$${f}\left({x}\right)=\mathrm{4}{x}+\mathrm{7} \\ $$
Commented by Zainal Arifin last updated on 14/Feb/20

$$\mathrm{You}\:\mathrm{are}\:\mathrm{Right}! \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
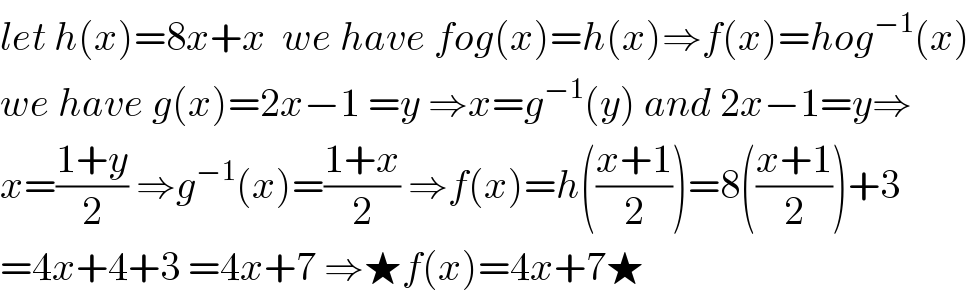
$${let}\:{h}\left({x}\right)=\mathrm{8}{x}+{x}\:\:{we}\:{have}\:{fog}\left({x}\right)={h}\left({x}\right)\Rightarrow{f}\left({x}\right)={hog}^{−\mathrm{1}} \left({x}\right) \\ $$$${we}\:{have}\:{g}\left({x}\right)=\mathrm{2}{x}−\mathrm{1}\:={y}\:\Rightarrow{x}={g}^{−\mathrm{1}} \left({y}\right)\:{and}\:\mathrm{2}{x}−\mathrm{1}={y}\Rightarrow \\ $$$${x}=\frac{\mathrm{1}+{y}}{\mathrm{2}}\:\Rightarrow{g}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{1}+{x}}{\mathrm{2}}\:\Rightarrow{f}\left({x}\right)={h}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)=\mathrm{8}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3} \\ $$$$=\mathrm{4}{x}+\mathrm{4}+\mathrm{3}\:=\mathrm{4}{x}+\mathrm{7}\:\Rightarrow\bigstar{f}\left({x}\right)=\mathrm{4}{x}+\mathrm{7}\bigstar \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20

$${h}\left({x}\right)=\mathrm{8}{x}+\mathrm{3} \\ $$
