Question Number 95520 by PRITHWISH SEN 2 last updated on 25/May/20
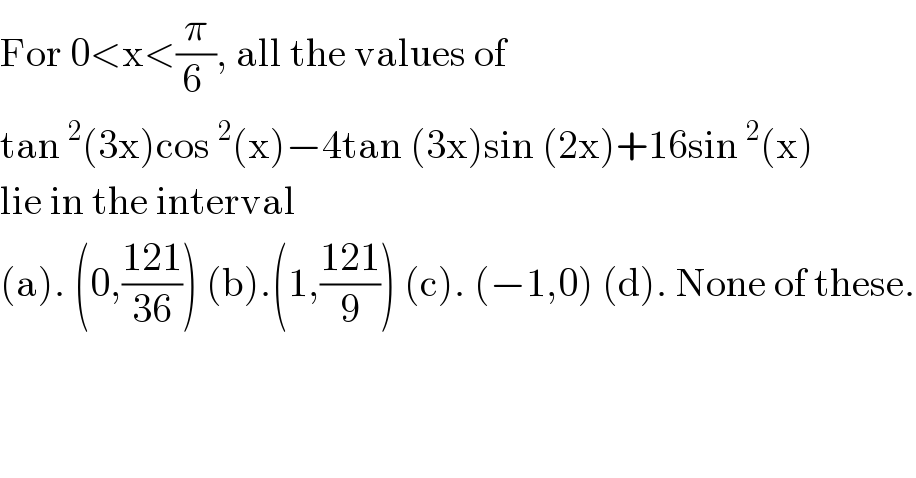
$$\mathrm{For}\:\mathrm{0}<\mathrm{x}<\frac{\pi}{\mathrm{6}\:},\:\mathrm{all}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of} \\ $$$$\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{3x}\right)\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{4tan}\:\left(\mathrm{3x}\right)\mathrm{sin}\:\left(\mathrm{2x}\right)+\mathrm{16sin}\:^{\mathrm{2}} \left(\mathrm{x}\right) \\ $$$$\mathrm{lie}\:\mathrm{in}\:\mathrm{the}\:\mathrm{interval} \\ $$$$\left(\mathrm{a}\right).\:\left(\mathrm{0},\frac{\mathrm{121}}{\mathrm{36}}\right)\:\left(\mathrm{b}\right).\left(\mathrm{1},\frac{\mathrm{121}}{\mathrm{9}}\right)\:\left(\mathrm{c}\right).\:\left(−\mathrm{1},\mathrm{0}\right)\:\left(\mathrm{d}\right).\:\mathrm{None}\:\mathrm{of}\:\mathrm{these}. \\ $$
