Question Number 102357 by Cynosure last updated on 08/Jul/20

$${for}\:{A}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7}\right\},{compute}\:{the}\:{number}\:{of}: \\ $$$$\left({a}\right)\:{Subsets}\:{of}\:{A}. \\ $$$$\left({b}\right)\:{Nonempty}\:{subsets}\:{of}\:{A}. \\ $$$$\left({c}\right)\:{proper}\:{subsets}\:{of}\:{A}. \\ $$$$\left({d}\right)\:{Non}\:{empty}\:{proper}\:{subset}\:{of}\:{A}. \\ $$$$\left({e}\right)\:{Subsets}\:{of}\:{A}\:{containing}\:{three}\:{element}. \\ $$$$\left({f}\right)\:{Subsets}\:{of}\:{A}\:{containing}\:\mathrm{1},\mathrm{2}. \\ $$$$\left({g}\right)\:{Proper}\:{subsets}\:{of}\:{A}\:{containing}\:\mathrm{1},\mathrm{2}. \\ $$$$\left({h}\right)\:{Subset}\:{of}\:{A}\:{with}\:{an}\:{even}\:{number}\:{of}\:{element}. \\ $$$$\left({i}\right)\:{Subset}\:{of}\:{A}\:{with}\:{an}\:{odd}\:{number}\:{of}\:{element}. \\ $$$$\left({j}\right)\:{Subsets}\:{of}\:{A}\:{with}\:{an}\:{odd}\:{number}\:{of}\:{elements},\:{including}\:{the}\:{element}\:\mathrm{3}. \\ $$
Answered by bobhans last updated on 09/Jul/20
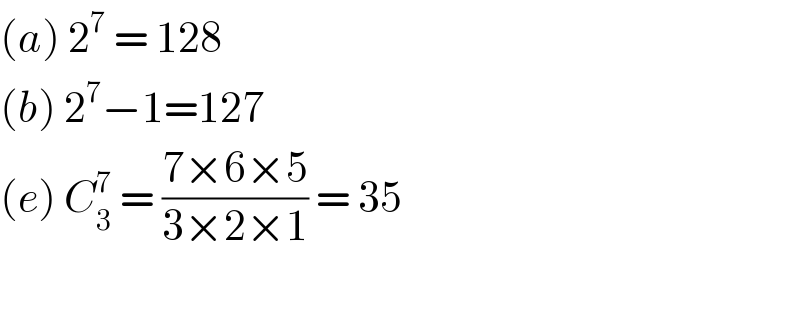
$$\left({a}\right)\:\mathrm{2}^{\mathrm{7}} \:=\:\mathrm{128} \\ $$$$\left({b}\right)\:\mathrm{2}^{\mathrm{7}} −\mathrm{1}=\mathrm{127} \\ $$$$\left({e}\right)\:{C}_{\mathrm{3}} ^{\mathrm{7}} \:=\:\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}\:=\:\mathrm{35} \\ $$$$ \\ $$
Commented by Cynosure last updated on 08/Jul/20
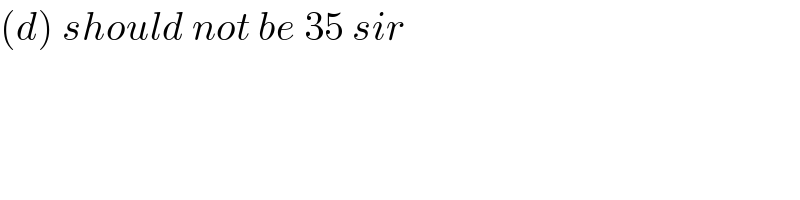
$$\left({d}\right)\:{should}\:{not}\:{be}\:\mathrm{35}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Jul/20
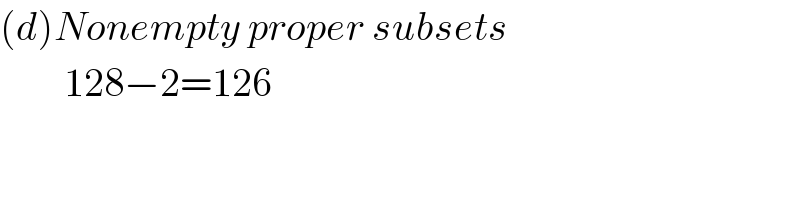
$$\left({d}\right){Nonempty}\:{proper}\:{subsets} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{128}−\mathrm{2}=\mathrm{126} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Jul/20
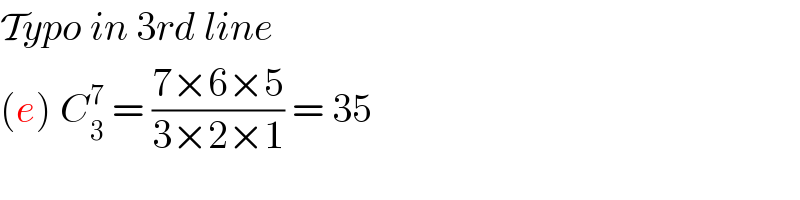
$$\mathcal{T}{ypo}\:{in}\:\mathrm{3}{rd}\:{line} \\ $$$$\left({e}\right)\:{C}_{\mathrm{3}} ^{\mathrm{7}} \:=\:\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}\:=\:\mathrm{35} \\ $$
Commented by bobhans last updated on 09/Jul/20
$${yes}\:{sir}.\:{thank}\:{you} \\ $$
Answered by bemath last updated on 09/Jul/20
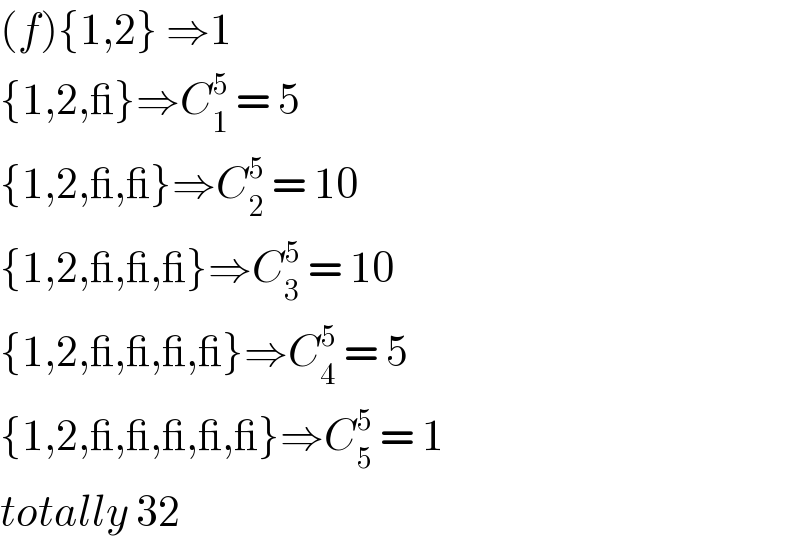
$$\left({f}\right)\left\{\mathrm{1},\mathrm{2}\right\}\:\Rightarrow\mathrm{1} \\ $$$$\left\{\mathrm{1},\mathrm{2},\_\right\}\Rightarrow{C}_{\mathrm{1}} ^{\mathrm{5}} \:=\:\mathrm{5} \\ $$$$\left\{\mathrm{1},\mathrm{2},\_,\_\right\}\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{5}} \:=\:\mathrm{10} \\ $$$$\left\{\mathrm{1},\mathrm{2},\_,\_,\_\right\}\Rightarrow{C}_{\mathrm{3}} ^{\mathrm{5}} \:=\:\mathrm{10} \\ $$$$\left\{\mathrm{1},\mathrm{2},\_,\_,\_,\_\right\}\Rightarrow{C}_{\mathrm{4}} ^{\mathrm{5}} \:=\:\mathrm{5} \\ $$$$\left\{\mathrm{1},\mathrm{2},\_,\_,\_,\_,\_\right\}\Rightarrow{C}_{\mathrm{5}} ^{\mathrm{5}} \:=\:\mathrm{1} \\ $$$${totally}\:\mathrm{32}\: \\ $$
