For-A-1-2-3-let-B-be-the-set-of-2-element-sets-belonging-to-P-A-and-let-C-be-the-set-consisting-of-the-sets-that-are-intersections-of-two-distinct-elements-of-B-Determine-C-P-A-power-set-

FacebookTweetPin

Question Number 42763 by Joel578 last updated on 02/Sep/18

$$\mathrm{For}A=\{1,2,3\},\mathrm{let}B\mathrm{be}\mathrm{the}\mathrm{set}\mathrm{of}2-\mathrm{element}\mathrm{sets}$$$$\mathrm{belonging}\mathrm{to}P\left(A\right)\mathrm{and}\mathrm{let}C\mathrm{be}\mathrm{the}\mathrm{set}\mathrm{consisting}\mathrm{of}$$$$\mathrm{the}\mathrm{sets}\mathrm{that}\mathrm{are}\mathrm{intersections}\mathrm{of}\mathrm{two}\mathrm{distinct}\mathrm{elements}$$$$\mathrm{of}B.\mathrm{Determine}C$$$$$$$$P\left(A\right)=\mathrm{power}\mathrm{set}\mathrm{of}A$$

Commented by Joel578 last updated on 02/Sep/18

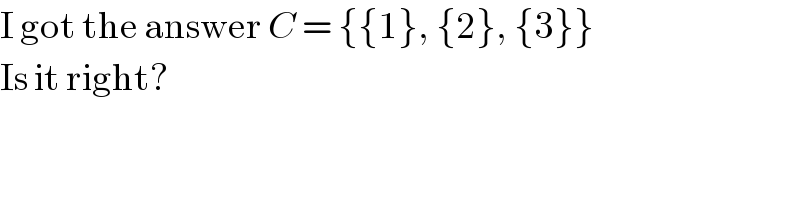
$$\mathrm{I}\mathrm{got}\mathrm{the}\mathrm{answer}C=\{\left\{1\right\},\left\{2\right\},\left\{3\right\}\}$$$$\mathrm{Is}\mathrm{it}\mathrm{right}?$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin