Menu Close

For-a-b-c-gt-0-Find-x-y-z-that-satisfy-this-equation-system-ax-by-x-y-2-by-cz-y-z-2-cz-ax-z-x-2-

Tinku Tara 0 Comments
Pin




Question Number 161071 by naka3546 last updated on 11/Dec/21
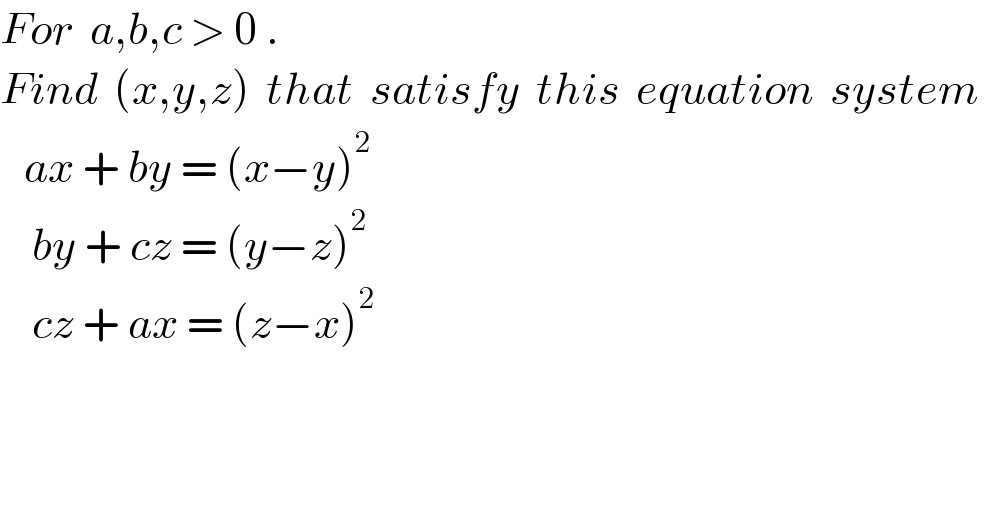
For a,b,c > 0 . Find (x,y,z) that satisfy this equation system ax + by = (x−y)^2 by + cz = (y−z)^2 cz + ax = (z−x)^2
$${For}\:\:{a},{b},{c}\:>\:\mathrm{0}\:. \\ $$$${Find}\:\:\left({x},{y},{z}\right)\:\:{that}\:\:{satisfy}\:\:{this}\:\:{equation}\:\:{system}\: \\ $$$$\:\:\:{ax}\:+\:{by}\:=\:\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:{by}\:+\:{cz}\:=\:\left({y}−{z}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:{cz}\:+\:{ax}\:=\:\left({z}−{x}\right)^{\mathrm{2}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 11/Dec/21
I think the only solution is x=y=z=0
$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:{x}={y}={z}=\mathrm{0} \\ $$
Commented by naka3546 last updated on 12/Dec/21
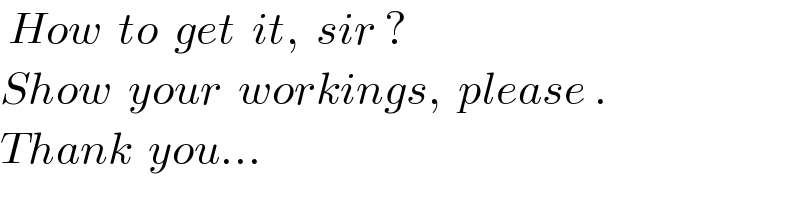
How to get it, sir ? Show your workings, please . Thank you...
$$\:{How}\:\:{to}\:\:{get}\:\:{it},\:\:{sir}\:? \\ $$$${Show}\:\:{your}\:\:{workings},\:\:{please}\:. \\ $$$${Thank}\:\:{you}… \\ $$
Answered by MJS_new last updated on 12/Dec/21
transformed equations x^2 −2xy+y^2 −ax−by=0 y^2 −2yz+z^2 −by−cz=0 x^2 −2xz+z^2 −ax−cz=0 each of these can be seen as a conic section. the 1^(st) is in the x−y−plane the 2^(nd) is in the y−z−plane the 3^(rd) is in the x−z−plane their only common point is (0∣0∣0)
$$\mathrm{transformed}\:\mathrm{equations} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} −{ax}−{by}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} −\mathrm{2}{yz}+{z}^{\mathrm{2}} −{by}−{cz}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{xz}+{z}^{\mathrm{2}} −{ax}−{cz}=\mathrm{0} \\ $$$$\mathrm{each}\:\mathrm{of}\:\mathrm{these}\:\mathrm{can}\:\mathrm{be}\:\mathrm{seen}\:\mathrm{as}\:\mathrm{a}\:\mathrm{conic}\:\mathrm{section}. \\ $$$$\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:{x}−{y}−\mathrm{plane} \\ $$$$\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:{y}−{z}−\mathrm{plane} \\ $$$$\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:{x}−{z}−\mathrm{plane} \\ $$$$\mathrm{their}\:\mathrm{only}\:\mathrm{common}\:\mathrm{point}\:\mathrm{is}\:\left(\mathrm{0}\mid\mathrm{0}\mid\mathrm{0}\right) \\ $$
Commented by MJS_new last updated on 12/Dec/21
you are right. pairs of the cones have common points in the axes
$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}.\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cones}\:\mathrm{have}\:\mathrm{common} \\ $$$$\mathrm{points}\:\mathrm{in}\:\mathrm{the}\:\mathrm{axes} \\ $$
Commented by mr W last updated on 12/Dec/21
i think other solutions are possible, e.g. (x,y,z)=(a, 0, 0) (x,y,z)=(0, b, 0) (x,y,z)=(0, 0, c) maybe that′s all.
$${i}\:{think}\:{other}\:{solutions}\:{are}\:{possible}, \\ $$$${e}.{g}.\: \\ $$$$\left({x},{y},{z}\right)=\left({a},\:\mathrm{0},\:\mathrm{0}\right) \\ $$$$\left({x},{y},{z}\right)=\left(\mathrm{0},\:{b},\:\mathrm{0}\right) \\ $$$$\left({x},{y},{z}\right)=\left(\mathrm{0},\:\mathrm{0},\:{c}\right) \\ $$$${maybe}\:{that}'{s}\:{all}. \\ $$
Commented by naka3546 last updated on 13/Dec/21
Thank you so much, sir.
$${Thank}\:\:{you}\:\:{so}\:\:{much},\:\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *