for-a-b-c-gt-0-prove-that-ab-bc-ca-2-3-a-b-c-abc-

Question Number 17260 by Umar math last updated on 03/Jul/17

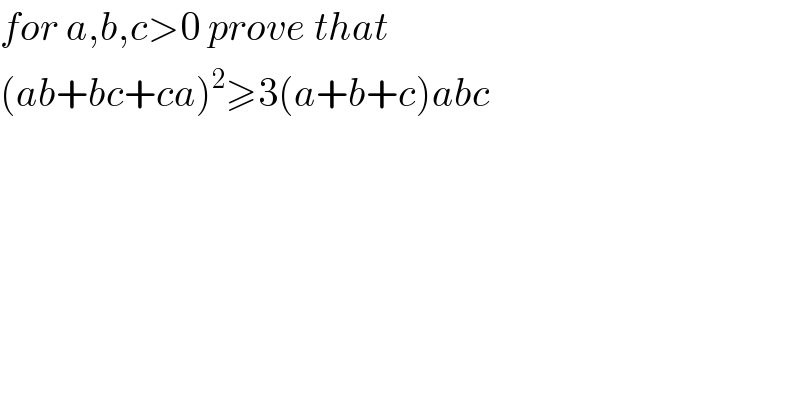
f o r a, b, c > 0 p r o v e t h a t

{(a b + b c + c a)}^{2} ⩾ 3 (a + b + c) a b c

Commented by prakash jain last updated on 03/Jul/17

As expained in answer by 18 ? 1 .

The condition a, b, c > 0 is never used .

Answered by 18±1 last updated on 05/Jul/17

x = a b, y = b c, z = c a

\Leftrightarrow {(x + y + z)}^{2} ⩾ 3 (x y + y z + z x)

\Leftrightarrow x^{2} + y^{2} + z^{2} ⩾ x y + y z + z x

\Leftrightarrow {(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2} ⩾ 0

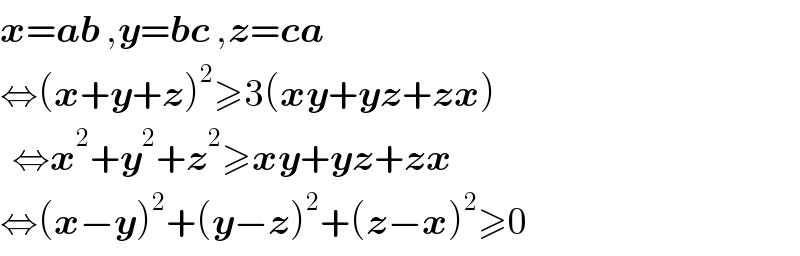
Commented by 18±1 last updated on 03/Jul/17

s o r r y 3 (x y + y z + z x) n o t a, b, c

Commented by Umar math last updated on 03/Jul/17

t h a n k y o u s i r, b u t a m k i n d o f c o n f u s e d .

Commented by 1234Hello last updated on 03/Jul/17

I am in doubt that the result is proved

or not ?!

Commented by prakash jain last updated on 03/Jul/17

Explaination of above answer

{(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2} ⩾ 0

\Rightarrow x^{2} - 2 x y + y^{2} + y^{2} - 2 y z + z^{2} + x^{2} - 2 x y ⩾ 0

\Rightarrow 2 (x^{2} + y^{2} + z^{2}) ⩾ 2 (x y + y z + z x)

\Rightarrow x^{2} + y^{2} + z^{2} ⩾ x y + y z + z x

\Rightarrow x^{2} + y^{2} + z^{2} + 2 x y + 2 y z + 2 z x ⩾ x y + y z

+ z x + 2 x y + 2 y z + 2 z x

\Rightarrow {(x + y + z)}^{2} ⩾ 3 (x y + y z + z x)

Now put x = a b, y = b c, z = c a

{(a b + b c + c a)}^{2} ⩾ 3 a b c (a + b + c)

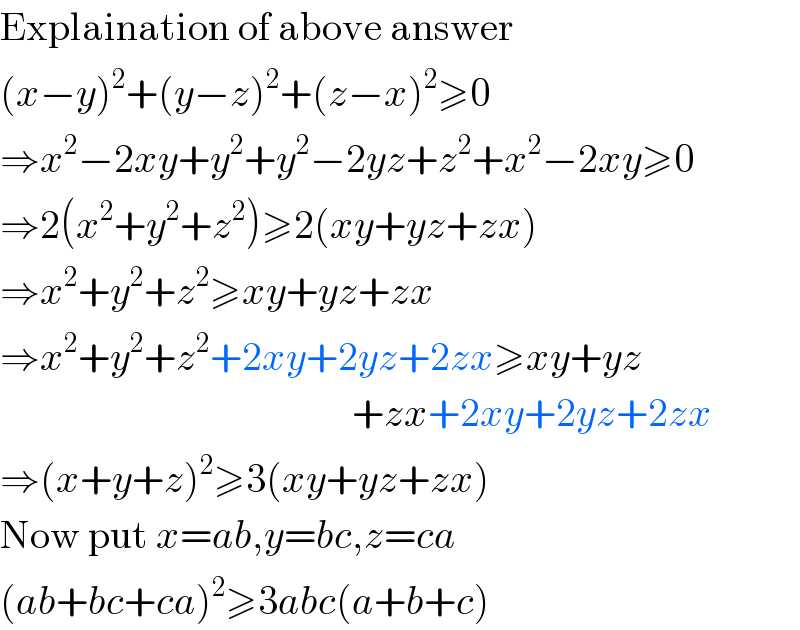
Commented by Umar math last updated on 03/Jul/17

t h a n k s a b u n c h s i r, a m c l e a r k n o w

Commented by Tinkutara last updated on 04/Jul/17

Thanks Sir!