Question Number 25937 by Mr eaay last updated on 16/Dec/17

$${For}\:{a}\:{certain}\:{amount}\:{of}\:{work},{Ade}\:{takes} \\ $$$$\mathrm{6}{hours}\:{less}\:{than}\:{Bode}.{if}\:{they}\:{work}\:{together} \\ $$$${it}\:{takes}\:{them}\:\mathrm{13}{hours}\:\mathrm{20}\:{minutes}.{How} \\ $$$${long}\:{will}\:{it}\:{take}\:{Bode}\:{alone}\:{to}\:{complete} \\ $$$${the}\:{work}? \\ $$
Answered by ajfour last updated on 16/Dec/17
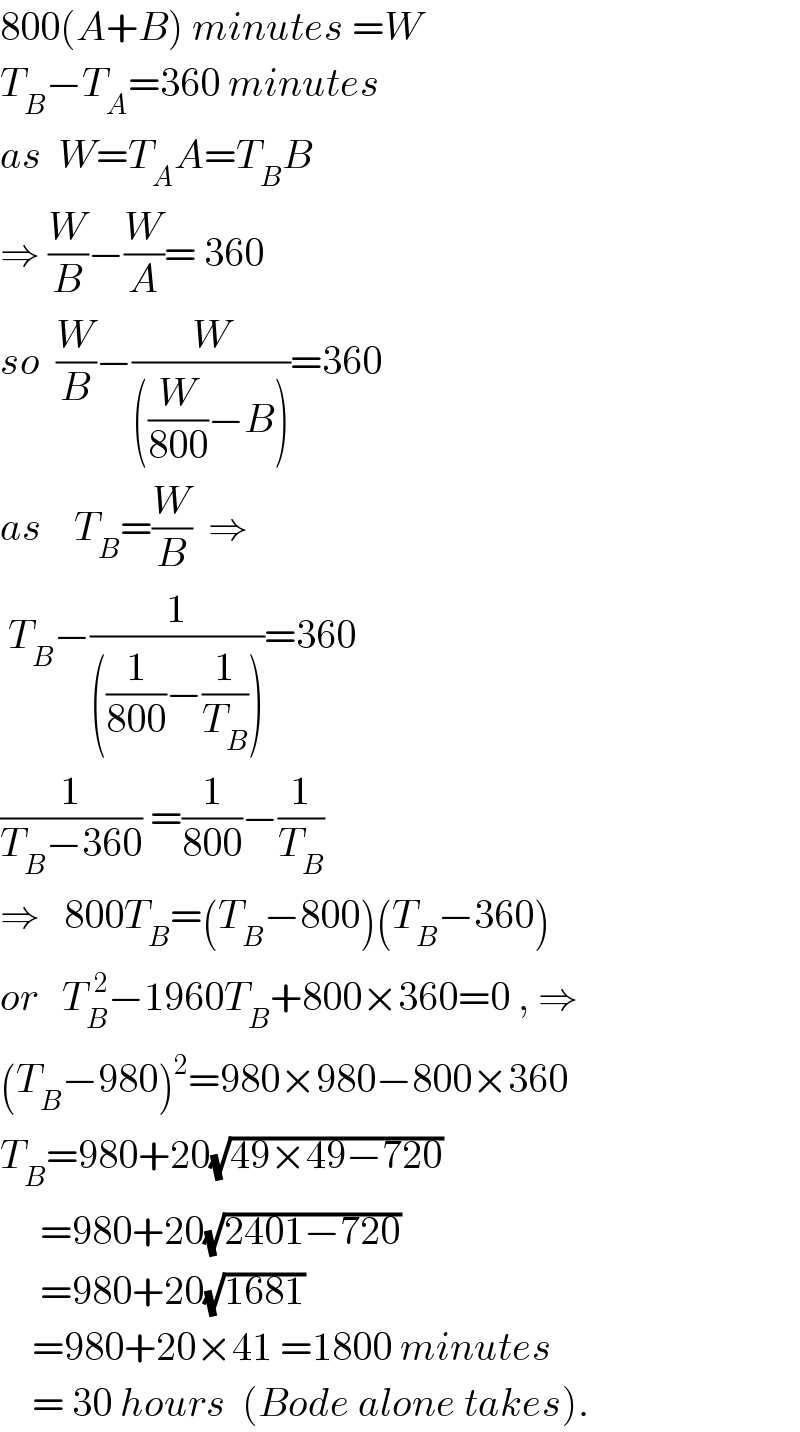
$$\mathrm{800}\left({A}+{B}\right)\:{minutes}\:={W} \\ $$$${T}_{{B}} −{T}_{{A}} =\mathrm{360}\:{minutes} \\ $$$${as}\:\:{W}={T}_{{A}} {A}={T}_{{B}} {B} \\ $$$$\Rightarrow\:\frac{{W}}{{B}}−\frac{{W}}{{A}}=\:\mathrm{360} \\ $$$${so}\:\:\frac{{W}}{{B}}−\frac{{W}}{\left(\frac{{W}}{\mathrm{800}}−{B}\right)}=\mathrm{360} \\ $$$${as}\:\:\:\:{T}_{{B}} =\frac{{W}}{{B}}\:\:\Rightarrow \\ $$$$\:{T}_{{B}} −\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\mathrm{800}}−\frac{\mathrm{1}}{{T}_{{B}} }\right)}=\mathrm{360} \\ $$$$\frac{\mathrm{1}}{{T}_{{B}} −\mathrm{360}}\:=\frac{\mathrm{1}}{\mathrm{800}}−\frac{\mathrm{1}}{{T}_{{B}} } \\ $$$$\Rightarrow\:\:\:\mathrm{800}{T}_{{B}} =\left({T}_{{B}} −\mathrm{800}\right)\left({T}_{{B}} −\mathrm{360}\right) \\ $$$${or}\:\:\:{T}_{{B}} ^{\:\:\mathrm{2}} −\mathrm{1960}{T}_{{B}} +\mathrm{800}×\mathrm{360}=\mathrm{0}\:,\:\Rightarrow \\ $$$$\left({T}_{{B}} −\mathrm{980}\right)^{\mathrm{2}} =\mathrm{980}×\mathrm{980}−\mathrm{800}×\mathrm{360} \\ $$$${T}_{{B}} =\mathrm{980}+\mathrm{20}\sqrt{\mathrm{49}×\mathrm{49}−\mathrm{720}} \\ $$$$\:\:\:\:\:=\mathrm{980}+\mathrm{20}\sqrt{\mathrm{2401}−\mathrm{720}} \\ $$$$\:\:\:\:\:=\mathrm{980}+\mathrm{20}\sqrt{\mathrm{1681}} \\ $$$$\:\:\:\:=\mathrm{980}+\mathrm{20}×\mathrm{41}\:=\mathrm{1800}\:{minutes} \\ $$$$\:\:\:\:=\:\mathrm{30}\:{hours}\:\:\left({Bode}\:{alone}\:{takes}\right). \\ $$
