Question Number 19799 by Tinkutara last updated on 15/Aug/17
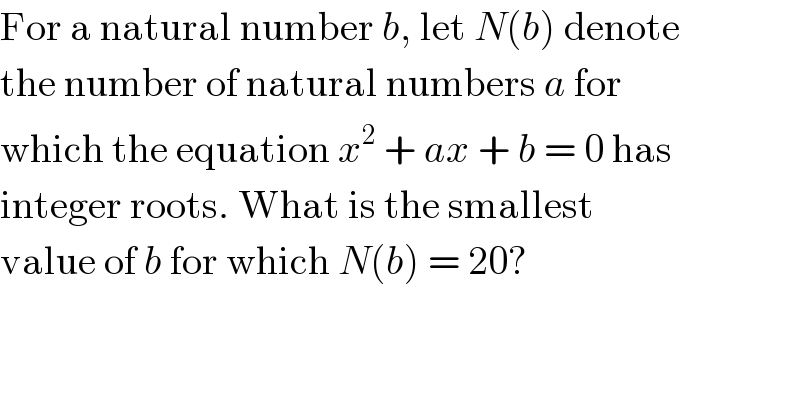
$$\mathrm{For}\:\mathrm{a}\:\mathrm{natural}\:\mathrm{number}\:{b},\:\mathrm{let}\:{N}\left({b}\right)\:\mathrm{denote} \\ $$$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{natural}\:\mathrm{numbers}\:{a}\:\mathrm{for} \\ $$$$\mathrm{which}\:\mathrm{the}\:\mathrm{equation}\:{x}^{\mathrm{2}} \:+\:{ax}\:+\:{b}\:=\:\mathrm{0}\:\mathrm{has} \\ $$$$\mathrm{integer}\:\mathrm{roots}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{smallest} \\ $$$$\mathrm{value}\:\mathrm{of}\:{b}\:\mathrm{for}\:\mathrm{which}\:{N}\left({b}\right)\:=\:\mathrm{20}? \\ $$
Commented by dioph last updated on 16/Aug/17
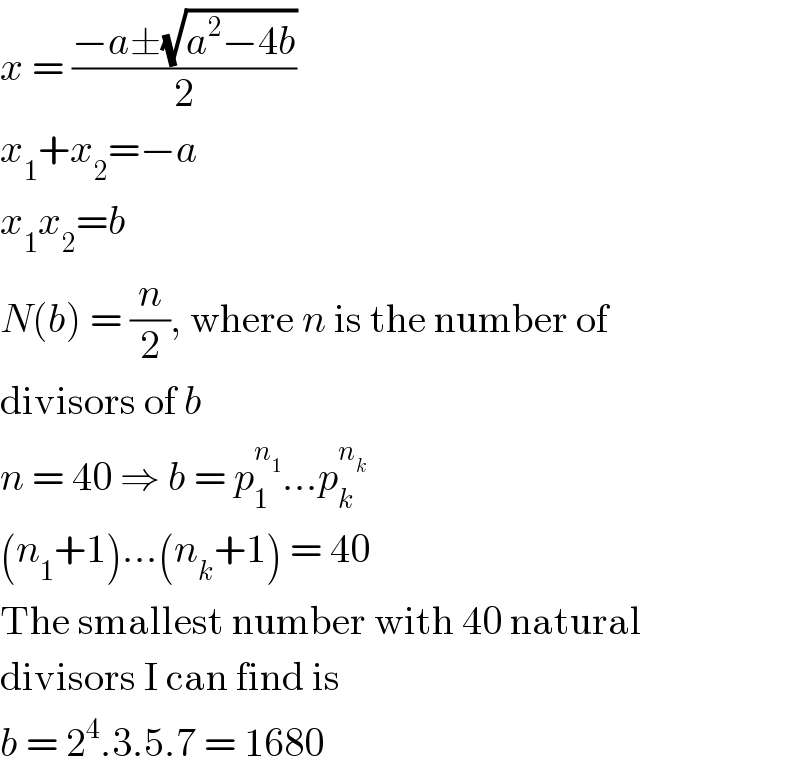
$${x}\:=\:\frac{−{a}\pm\sqrt{{a}^{\mathrm{2}} −\mathrm{4}{b}}}{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =−{a} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} ={b} \\ $$$${N}\left({b}\right)\:=\:\frac{{n}}{\mathrm{2}},\:\mathrm{where}\:{n}\:\mathrm{is}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{divisors}\:\mathrm{of}\:{b} \\ $$$${n}\:=\:\mathrm{40}\:\Rightarrow\:{b}\:=\:{p}_{\mathrm{1}} ^{{n}_{\mathrm{1}} } …{p}_{{k}} ^{{n}_{{k}} } \\ $$$$\left({n}_{\mathrm{1}} +\mathrm{1}\right)…\left({n}_{{k}} +\mathrm{1}\right)\:=\:\mathrm{40} \\ $$$$\mathrm{The}\:\mathrm{smallest}\:\mathrm{number}\:\mathrm{with}\:\mathrm{40}\:\mathrm{natural} \\ $$$$\mathrm{divisors}\:\mathrm{I}\:\mathrm{can}\:\mathrm{find}\:\mathrm{is} \\ $$$${b}\:=\:\mathrm{2}^{\mathrm{4}} .\mathrm{3}.\mathrm{5}.\mathrm{7}\:=\:\mathrm{1680} \\ $$
Commented by Tinkutara last updated on 16/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
