Question Number 128459 by SLVR last updated on 07/Jan/21
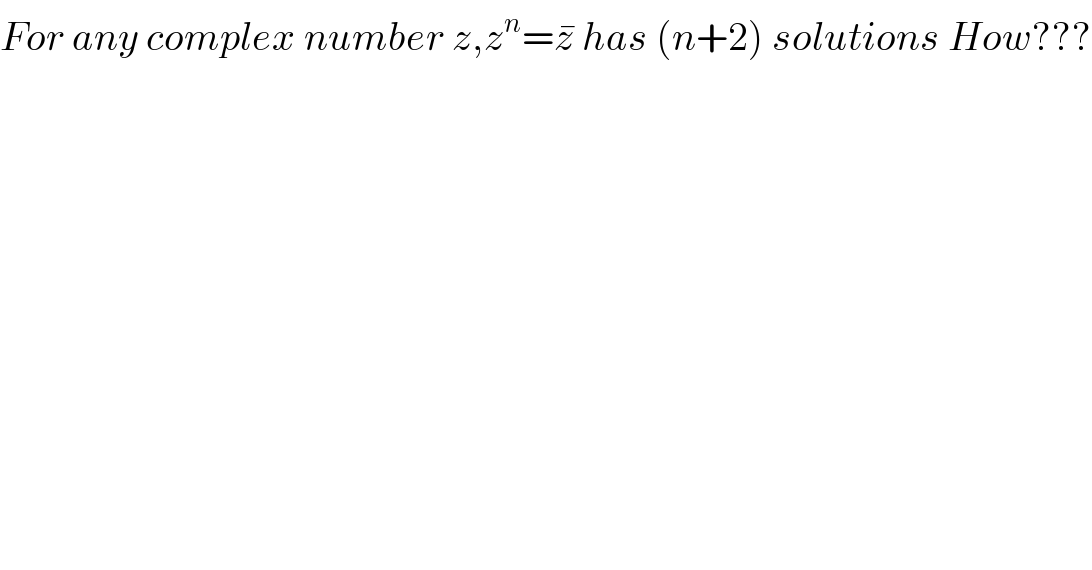
$${For}\:{any}\:{complex}\:{number}\:{z},{z}^{{n}} =\bar {{z}}\:{has}\:\left({n}+\mathrm{2}\right)\:{solutions}\:{How}??? \\ $$
Answered by mr W last updated on 10/Jan/21
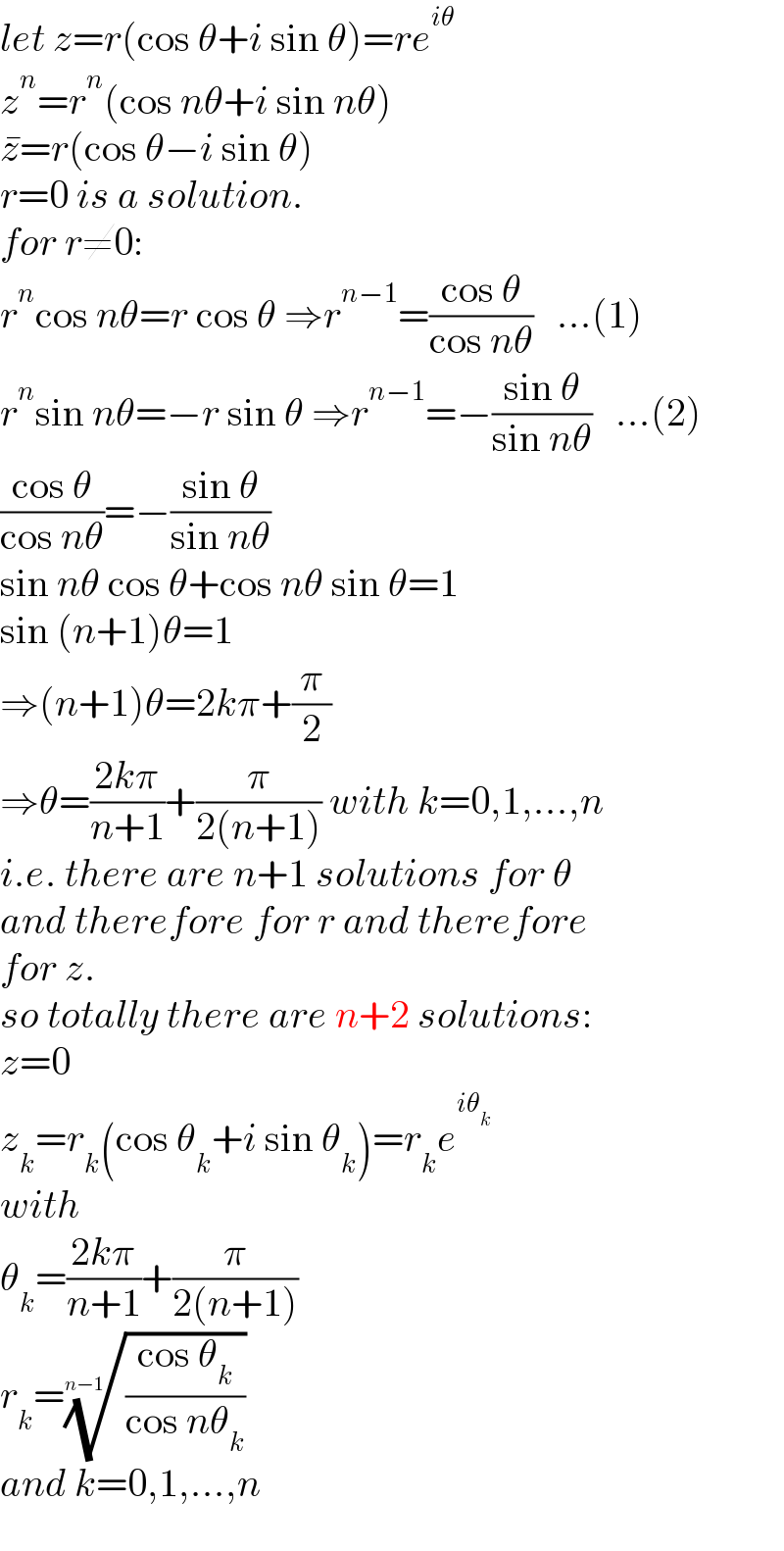
$${let}\:{z}={r}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right)={re}^{{i}\theta} \\ $$$${z}^{{n}} ={r}^{{n}} \left(\mathrm{cos}\:{n}\theta+{i}\:\mathrm{sin}\:{n}\theta\right) \\ $$$$\bar {{z}}={r}\left(\mathrm{cos}\:\theta−{i}\:\mathrm{sin}\:\theta\right) \\ $$$${r}=\mathrm{0}\:{is}\:{a}\:{solution}. \\ $$$${for}\:{r}\neq\mathrm{0}: \\ $$$${r}^{{n}} \mathrm{cos}\:{n}\theta={r}\:\mathrm{cos}\:\theta\:\Rightarrow{r}^{{n}−\mathrm{1}} =\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:{n}\theta}\:\:\:…\left(\mathrm{1}\right) \\ $$$${r}^{{n}} \mathrm{sin}\:{n}\theta=−{r}\:\mathrm{sin}\:\theta\:\Rightarrow{r}^{{n}−\mathrm{1}} =−\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:{n}\theta}\:\:\:…\left(\mathrm{2}\right) \\ $$$$\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:{n}\theta}=−\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:{n}\theta}\: \\ $$$$\mathrm{sin}\:{n}\theta\:\mathrm{cos}\:\theta+\mathrm{cos}\:{n}\theta\:\mathrm{sin}\:\theta=\mathrm{1} \\ $$$$\mathrm{sin}\:\left({n}+\mathrm{1}\right)\theta=\mathrm{1} \\ $$$$\Rightarrow\left({n}+\mathrm{1}\right)\theta=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\frac{\mathrm{2}{k}\pi}{{n}+\mathrm{1}}+\frac{\pi}{\mathrm{2}\left({n}+\mathrm{1}\right)}\:{with}\:{k}=\mathrm{0},\mathrm{1},…,{n} \\ $$$${i}.{e}.\:{there}\:{are}\:{n}+\mathrm{1}\:{solutions}\:{for}\:\theta \\ $$$${and}\:{therefore}\:{for}\:{r}\:{and}\:{therefore} \\ $$$${for}\:{z}. \\ $$$${so}\:{totally}\:{there}\:{are}\:{n}+\mathrm{2}\:{solutions}: \\ $$$${z}=\mathrm{0} \\ $$$${z}_{{k}} ={r}_{{k}} \left(\mathrm{cos}\:\theta_{{k}} +{i}\:\mathrm{sin}\:\theta_{{k}} \right)={r}_{{k}} {e}^{{i}\theta_{{k}} } \\ $$$${with} \\ $$$$\theta_{{k}} =\frac{\mathrm{2}{k}\pi}{{n}+\mathrm{1}}+\frac{\pi}{\mathrm{2}\left({n}+\mathrm{1}\right)} \\ $$$${r}_{{k}} =\sqrt[{{n}−\mathrm{1}}]{\frac{\mathrm{cos}\:\theta_{{k}} }{\mathrm{cos}\:{n}\theta_{{k}} }} \\ $$$${and}\:{k}=\mathrm{0},\mathrm{1},…,{n} \\ $$
