Question Number 94954 by Mr.D.N. last updated on 22/May/20
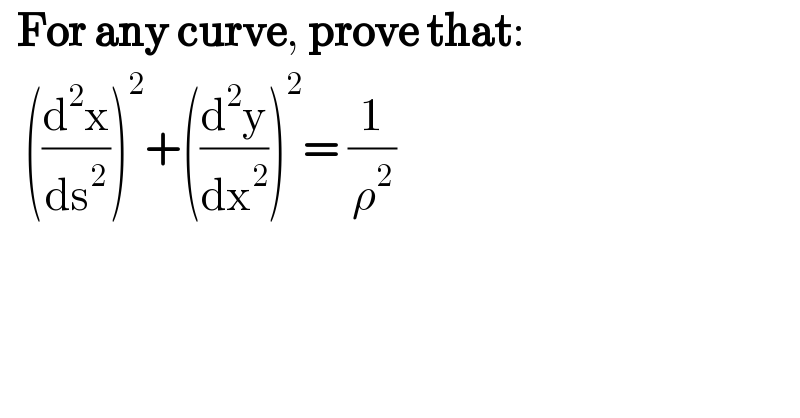
$$\:\:\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{any}}\:\boldsymbol{\mathrm{curve}},\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}: \\ $$$$\:\:\:\left(\frac{\mathrm{d}^{\mathrm{2}} \mathrm{x}}{\mathrm{ds}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\right)^{\mathrm{2}} =\:\frac{\mathrm{1}}{\rho^{\mathrm{2}} } \\ $$$$\:\: \\ $$
Answered by niroj last updated on 22/May/20
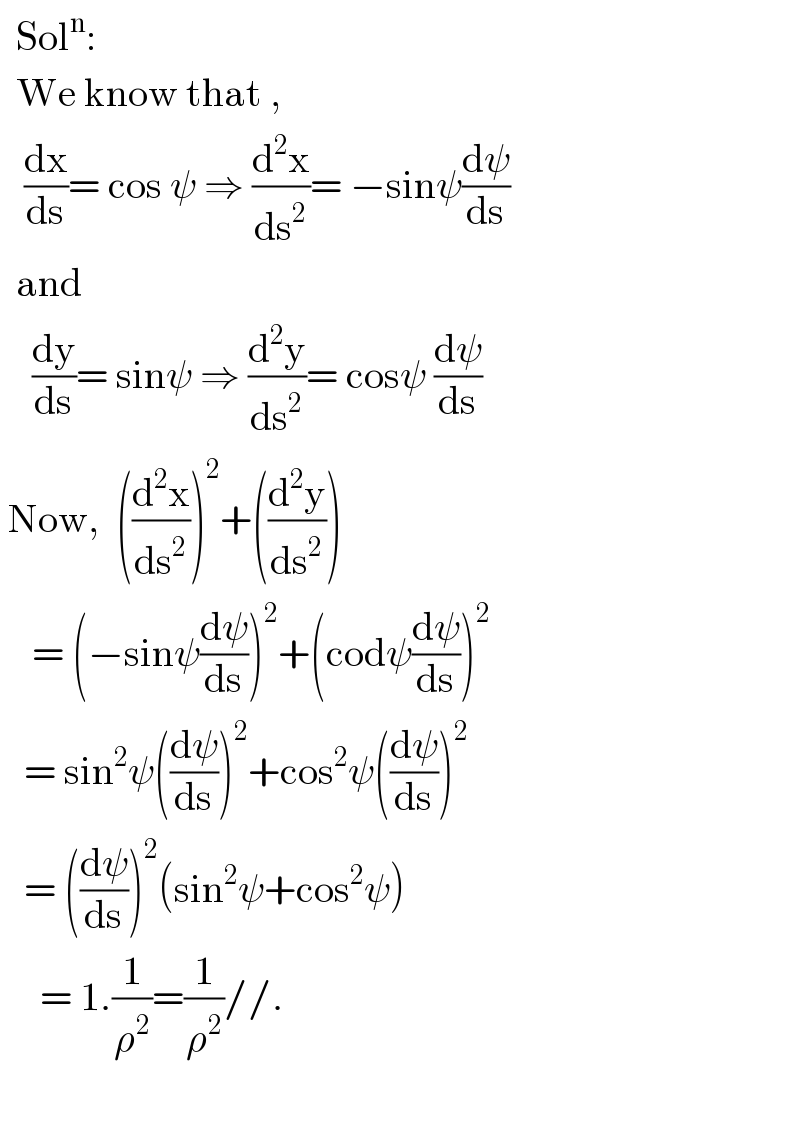
$$\:\:\mathrm{Sol}^{\mathrm{n}} : \\ $$$$\:\:\mathrm{We}\:\mathrm{know}\:\mathrm{that}\:, \\ $$$$\:\:\:\frac{\mathrm{dx}}{\mathrm{ds}}=\:\mathrm{cos}\:\psi\:\Rightarrow\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{x}}{\mathrm{ds}^{\mathrm{2}} }=\:−\mathrm{sin}\psi\frac{\mathrm{d}\psi}{\mathrm{ds}} \\ $$$$\:\:\mathrm{and} \\ $$$$\:\:\:\:\frac{\mathrm{dy}}{\mathrm{ds}}=\:\mathrm{sin}\psi\:\Rightarrow\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{ds}^{\mathrm{2}} }=\:\mathrm{cos}\psi\:\frac{\mathrm{d}\psi}{\mathrm{ds}} \\ $$$$\:\mathrm{Now},\:\:\left(\frac{\mathrm{d}^{\mathrm{2}} \mathrm{x}}{\mathrm{ds}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{ds}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:=\:\left(−\mathrm{sin}\psi\frac{\mathrm{d}\psi}{\mathrm{ds}}\right)^{\mathrm{2}} +\left(\mathrm{cod}\psi\frac{\mathrm{d}\psi}{\mathrm{ds}}\right)^{\mathrm{2}} \\ $$$$\:\:\:=\:\mathrm{sin}^{\mathrm{2}} \psi\left(\frac{\mathrm{d}\psi}{\mathrm{ds}}\right)^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \psi\left(\frac{\mathrm{d}\psi}{\mathrm{ds}}\right)^{\mathrm{2}} \\ $$$$\:\:\:=\:\left(\frac{\mathrm{d}\psi}{\mathrm{ds}}\right)^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \psi+\mathrm{cos}^{\mathrm{2}} \psi\right) \\ $$$$\:\:\:\:\:=\:\mathrm{1}.\frac{\mathrm{1}}{\rho^{\mathrm{2}} }=\frac{\mathrm{1}}{\rho^{\mathrm{2}} }//. \\ $$$$\:\: \\ $$
Commented by Mr.D.N. last updated on 22/May/20
outstanding��✍
