for-any-two-complex-number-z-w-then-z-w-z-w-true-or-false-

Question Number 130639 by mohammad17 last updated on 27/Jan/21

f o r a n y t w o c o m p l e x n u m b e r (z, w) t h e n

\sqrt{z . w} = \sqrt{z} . \sqrt{w}

t r u e o r f a l s e

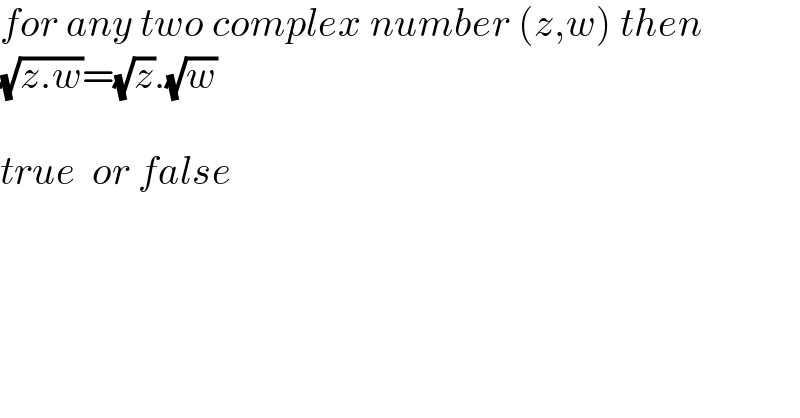
Commented by malwan last updated on 27/Jan/21

t h a n k y o u

Commented by mohammad17 last updated on 27/Jan/21

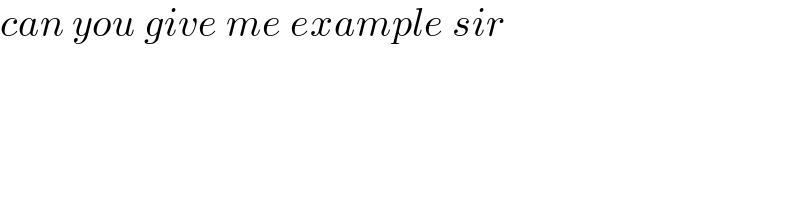
c a n y o u g i v e m e e x a m p l e s i r

Commented by mohammad17 last updated on 27/Jan/21

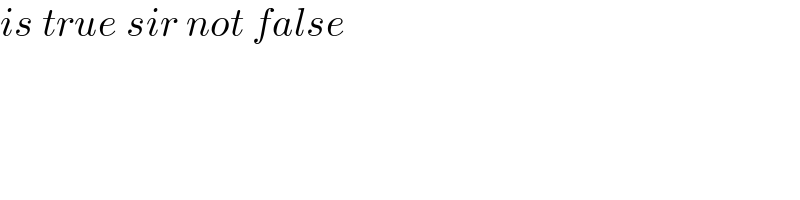
i s t r u e s i r n o t f a l s e

Answered by MJS_new last updated on 27/Jan/21

z = r e^{i α}; r ⩾ 0 \land 0 ⩽ α < 2 π

w = s e^{i β}; s ⩾ 0 \land 0 ⩽ β < 2 π

\sqrt{z} = \sqrt{r} e^{i \frac{α}{2}}

\sqrt{w} = \sqrt{s} e^{i \frac{β}{2}}

\sqrt{z} \sqrt{w} = \sqrt{r s} e^{i \frac{α + β}{2}}

\sqrt{z w} = \sqrt{r e^{i α} s e^{i β}} = \sqrt{r s e^{(α + β)}} = \sqrt{r s} e^{i \frac{α + β}{2}}

\Rightarrow true

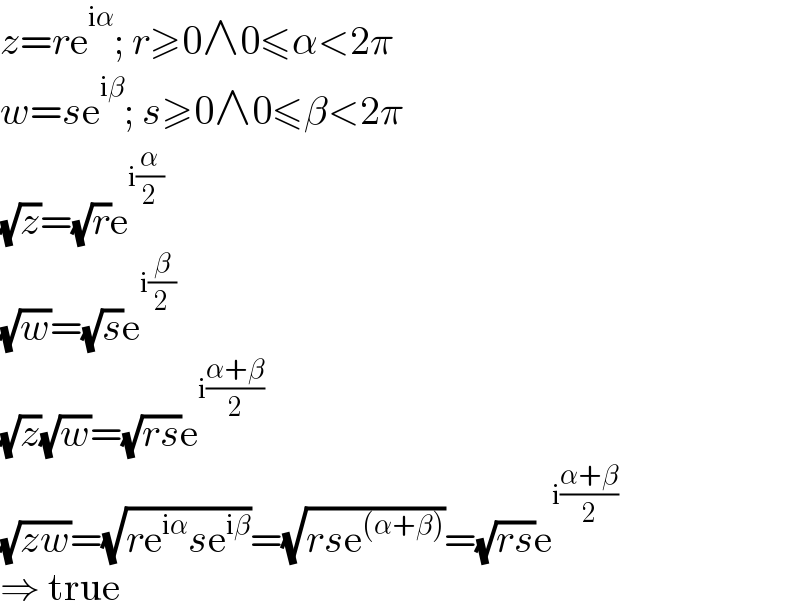
Commented by mohammad17 last updated on 27/Jan/21

t h a n k y o u s i r