Question Number 150402 by mathdanisur last updated on 12/Aug/21
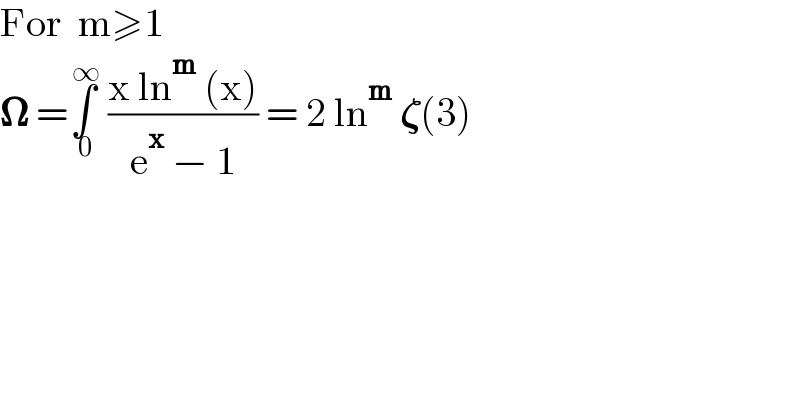
$$\mathrm{For}\:\:\mathrm{m}\geqslant\mathrm{1} \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{x}\:\mathrm{ln}^{\boldsymbol{\mathrm{m}}} \:\left(\mathrm{x}\right)}{\mathrm{e}^{\boldsymbol{\mathrm{x}}} \:−\:\mathrm{1}}\:=\:\mathrm{2}\:\mathrm{ln}^{\boldsymbol{\mathrm{m}}} \:\boldsymbol{\zeta}\left(\mathrm{3}\right) \\ $$
Commented by yadiirama last updated on 12/Aug/21

$$ \\ $$
Answered by Lordose last updated on 12/Aug/21
![𝛀 =∫_( 0) ^( ∞) ((x ln^m (x))/(e^x − 1)) = 2 ln^m 𝛇(3) Ω = ∫_0 ^( ∞) ((xln^m (x))/(e^x − 1))dx = ∫_0 ^( ∞) ((xe^(−x) ln^m (x))/(1−e^(−x) ))dx Ω = (∂^((m)) /∂a^((m)) )∫_0 ^( ∞) ((x^a e^(−x) )/(1−e^(−x) ))dx∣_(a=1) = (∂^((m)) /∂a^((m)) )Σ_(n=0) ^∞ ∫_0 ^( ∞) x^a e^(−x(n+1)) dx Ω =^(x=(x/(n+1))) [ (∂^((m)) /∂a^((m)) )Σ_(n=0) ^∞ (1/((n+1)^(a+1) ))∫_0 ^( ∞) x^(a+1−1) e^(−x) dx]_(a=1) Ω = (∂^((m)) /∂a^((m)) )(a!Σ_(n=0) ^∞ (1/((n+1)^(a+1) )))∣_(a=1) = [(∂^((m)) /∂a^((m)) )(𝚪(a+1)𝛇(a+1))]_(a=1) My try 𝛀 =∫_( 0) ^( ∞) ((x ln^m (x))/(e^x − 1)) = 2 ln^m 𝛇(3)](https://www.tinkutara.com/question/Q150443.png)
$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{x}\:\mathrm{ln}^{\boldsymbol{\mathrm{m}}} \:\left(\mathrm{x}\right)}{\mathrm{e}^{\boldsymbol{\mathrm{x}}} \:−\:\mathrm{1}}\:=\:\mathrm{2}\:\mathrm{ln}^{\boldsymbol{\mathrm{m}}} \:\boldsymbol{\zeta}\left(\mathrm{3}\right) \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{xln}^{\mathrm{m}} \left(\mathrm{x}\right)}{\mathrm{e}^{\mathrm{x}} \:−\:\mathrm{1}}\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{xe}^{−\mathrm{x}} \mathrm{ln}^{\mathrm{m}} \left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$\Omega\:=\:\frac{\partial^{\left(\mathrm{m}\right)} }{\partial\mathrm{a}^{\left(\mathrm{m}\right)} }\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{a}} \mathrm{e}^{−\mathrm{x}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{x}} }\mathrm{dx}\mid_{\mathrm{a}=\mathrm{1}} \:=\:\frac{\partial^{\left(\mathrm{m}\right)} }{\partial\mathrm{a}^{\left(\mathrm{m}\right)} }\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}} \mathrm{e}^{−\mathrm{x}\left(\mathrm{n}+\mathrm{1}\right)} \mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{x}=\frac{\mathrm{x}}{\mathrm{n}+\mathrm{1}}} {=}\left[\:\frac{\partial^{\left(\mathrm{m}\right)} \:}{\partial\mathrm{a}^{\left(\mathrm{m}\right)} }\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{a}+\mathrm{1}} }\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}+\mathrm{1}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx}\right]_{\mathrm{a}=\mathrm{1}} \\ $$$$\Omega\:=\:\frac{\partial^{\left(\mathrm{m}\right)} }{\partial\mathrm{a}^{\left(\mathrm{m}\right)} }\left(\mathrm{a}!\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{a}+\mathrm{1}} }\right)\mid_{\mathrm{a}=\mathrm{1}} \:=\:\left[\frac{\partial^{\left(\mathrm{m}\right)} }{\partial\mathrm{a}^{\left(\mathrm{m}\right)} }\left(\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right)\boldsymbol{\zeta}\left(\mathrm{a}+\mathrm{1}\right)\right)\right]_{\mathrm{a}=\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{My}\:\mathrm{try} \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{x}\:\mathrm{ln}^{\boldsymbol{\mathrm{m}}} \:\left(\mathrm{x}\right)}{\mathrm{e}^{\boldsymbol{\mathrm{x}}} \:−\:\mathrm{1}}\:=\:\mathrm{2}\:\mathrm{ln}^{\boldsymbol{\mathrm{m}}} \:\boldsymbol{\zeta}\left(\mathrm{3}\right) \\ $$$$ \\ $$
