Question Number 100677 by bobhans last updated on 28/Jun/20
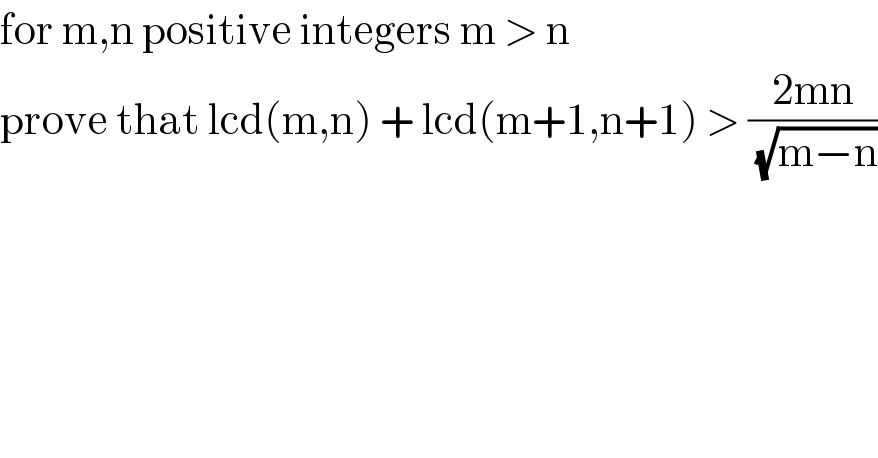
$$\mathrm{for}\:\mathrm{m},\mathrm{n}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{m}\:>\:\mathrm{n}\: \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{lcd}\left(\mathrm{m},\mathrm{n}\right)\:+\:\mathrm{lcd}\left(\mathrm{m}+\mathrm{1},\mathrm{n}+\mathrm{1}\right)\:>\:\frac{\mathrm{2mn}}{\:\sqrt{\mathrm{m}−\mathrm{n}}} \\ $$
