Question Number 13295 by Tinkutara last updated on 17/May/17
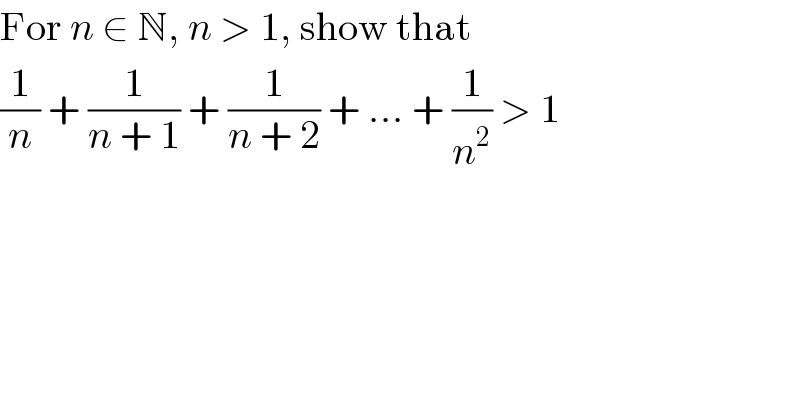
$$\mathrm{For}\:{n}\:\in\:\mathbb{N},\:{n}\:>\:\mathrm{1},\:\mathrm{show}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{{n}}\:+\:\frac{\mathrm{1}}{{n}\:+\:\mathrm{1}}\:+\:\frac{\mathrm{1}}{{n}\:+\:\mathrm{2}}\:+\:…\:+\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:>\:\mathrm{1} \\ $$
Commented by prakash jain last updated on 17/May/17

$${n}=\mathrm{2}\:{and}\:\mathrm{3}\:{can}\:{be}\:{checked} \\ $$$${with}\:{hand}\:{calculation} \\ $$$${n}\geqslant\mathrm{4} \\ $$$${n}^{\mathrm{2}} \geqslant\mathrm{4}{n} \\ $$$$\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}+….+\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$>\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+…..+\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+..+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:+\:\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}+…+\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{3}{n}}+\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{1}}+….+\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{1}} \\ $$$$>\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}+…+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{1}}+….+\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{1}}+…+\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{1}} \\ $$$$=\frac{{n}}{\mathrm{2}{n}−\mathrm{1}}+\frac{{n}}{\mathrm{3}{n}−\mathrm{1}}+\frac{{n}}{\mathrm{4}{n}−\mathrm{1}} \\ $$$$>\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}>\mathrm{1} \\ $$
Commented by Tinkutara last updated on 18/May/17
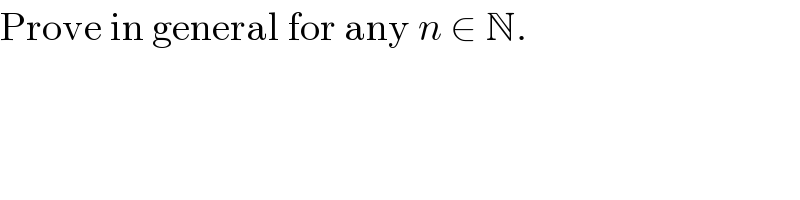
$$\mathrm{Prove}\:\mathrm{in}\:\mathrm{general}\:\mathrm{for}\:\mathrm{any}\:{n}\:\in\:\mathbb{N}. \\ $$
Commented by prakash jain last updated on 18/May/17
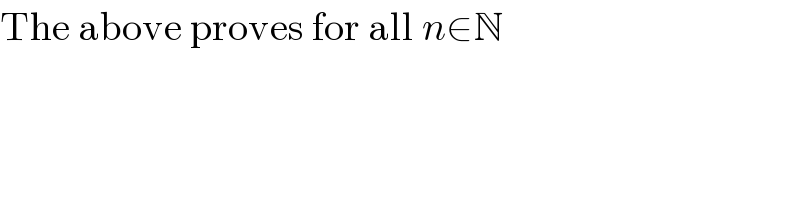
$$\mathrm{The}\:\mathrm{above}\:\mathrm{proves}\:\mathrm{for}\:\mathrm{all}\:{n}\in\mathbb{N} \\ $$
Answered by mrW1 last updated on 18/May/17

$${Just}\:{to}\:{play}…… \\ $$$$ \\ $$$${There}\:{are}\:{n}^{\mathrm{2}} −{n}+\mathrm{1}\:{terms}\:{in}\:{total}. \\ $$$${n}^{\mathrm{2}} −{n}+\mathrm{1}=\left({n}−\mathrm{1}\right){n}+\mathrm{1} \\ $$$$\Rightarrow{we}\:{can}\:{sort}\:{the}\:{terms}\:{in}\:{n}\:{groups}: \\ $$$${group}\:\mathrm{1}\:{with}\:{n}\:{terms}: \\ $$$${S}_{\mathrm{1}} =\frac{\mathrm{1}}{{n}}\:+\:\frac{\mathrm{1}}{{n}\:+\:\mathrm{1}}\:+\:\frac{\mathrm{1}}{{n}\:+\:\mathrm{2}}\:+\:…\:+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}} \\ $$$${group}\:\mathrm{2}\:{with}\:{n}\:{terms}: \\ $$$${S}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}{n}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{n}\:+\:\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{n}\:+\:\mathrm{2}}\:+\:…\:+\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{1}} \\ $$$$…… \\ $$$${group}\:{k}\:{with}\:{n}\:{terms}: \\ $$$${S}_{{k}} =\frac{\mathrm{1}}{{kn}}\:+\:\frac{\mathrm{1}}{{kn}\:+\:\mathrm{1}}\:+\:\frac{\mathrm{1}}{{kn}\:+\:\mathrm{2}}\:+\:…\:+\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){n}−\mathrm{1}} \\ $$$$…… \\ $$$${group}\:{n}−\mathrm{1}\:{with}\:{n}\:{terms}: \\ $$$${S}_{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right){n}}\:+\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right){n}\:+\:\mathrm{1}}\:+\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right){n}\:+\:\mathrm{2}}\:+\:…\:+\frac{\mathrm{1}}{{n}×{n}−\mathrm{1}} \\ $$$${group}\:{n}\:{with}\:\mathrm{1}\:{term}: \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$ \\ $$$${sum}\:{of}\:{terms}\:{in}\:{group}\:{k}: \\ $$$${S}_{{k}} =\frac{\mathrm{1}}{{kn}}\:+\:\frac{\mathrm{1}}{{kn}\:+\:\mathrm{1}}\:+\:\frac{\mathrm{1}}{{kn}\:+\:\mathrm{2}}\:+\:…\:+\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){n}−\mathrm{1}} \\ $$$$>{n}×\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){n}−\mathrm{1}}>\frac{{n}}{\left({k}+\mathrm{1}\right){n}}=\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$ \\ $$$${sum}\:{of}\:{all}\:{terms}: \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{S}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{S}_{{k}} +{S}_{{n}} \\ $$$$>\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{1}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1} \\ $$$${for}\:{big}\:{number}\:{n}: \\ $$$${S}>\mathrm{ln}\:{n}+\gamma+\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{12}{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}\:\:{with}\:\gamma=\mathrm{0}.\mathrm{57721}… \\ $$$${S}>\mathrm{ln}\:{n}+\gamma+\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{11}}{\mathrm{12}{n}^{\mathrm{2}} }−\mathrm{1} \\ $$
Commented by prakash jain last updated on 18/May/17
![γ=lim_(n→∞) [Σ_(i=1) ^n (1/i)−ln n]](https://www.tinkutara.com/question/Q13318.png)
$$\gamma=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{i}}−\mathrm{ln}\:{n}\right] \\ $$
Commented by mrW1 last updated on 18/May/17
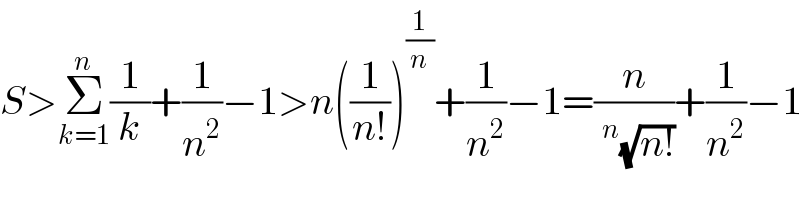
$${S}>\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}>{n}\left(\frac{\mathrm{1}}{{n}!}\right)^{\frac{\mathrm{1}}{{n}}} +\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}=\frac{{n}}{\:^{{n}} \sqrt{{n}!}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1} \\ $$
