For-natural-numbers-x-and-y-let-x-y-denote-the-greatest-common-divisor-of-x-and-y-How-many-pairs-of-natural-numbers-x-and-y-with-x-y-satisfy-the-equation-xy-x-y-x-y-

FacebookTweetPin

Question Number 19786 by Tinkutara last updated on 15/Aug/17

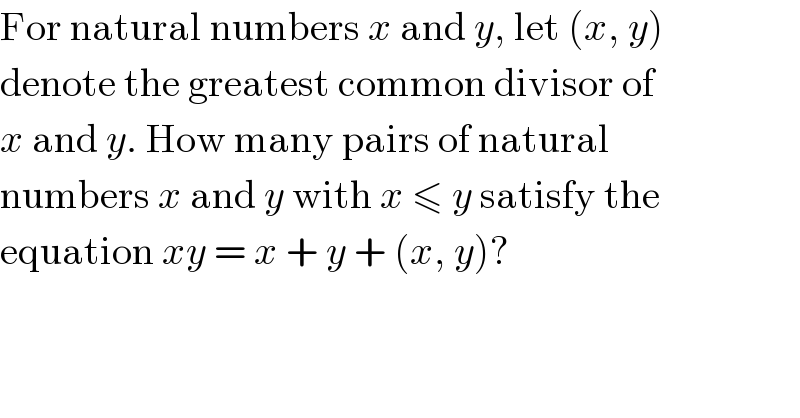
$$\mathrm{For}\mathrm{natural}\mathrm{numbers}x\mathrm{and}y,\mathrm{let}(x,y)$$$$\mathrm{denote}\mathrm{the}\mathrm{greatest}\mathrm{common}\mathrm{divisor}\mathrm{of}$$$$x\mathrm{and}y.\mathrm{How}\mathrm{many}\mathrm{pairs}\mathrm{of}\mathrm{natural}$$$$\mathrm{numbers}x\mathrm{and}y\mathrm{with}x⩽y\mathrm{satisfy}\mathrm{the}$$$$\mathrm{equation}xy=x+y+(x,y)?$$

Answered by mrW1 last updated on 16/Aug/17

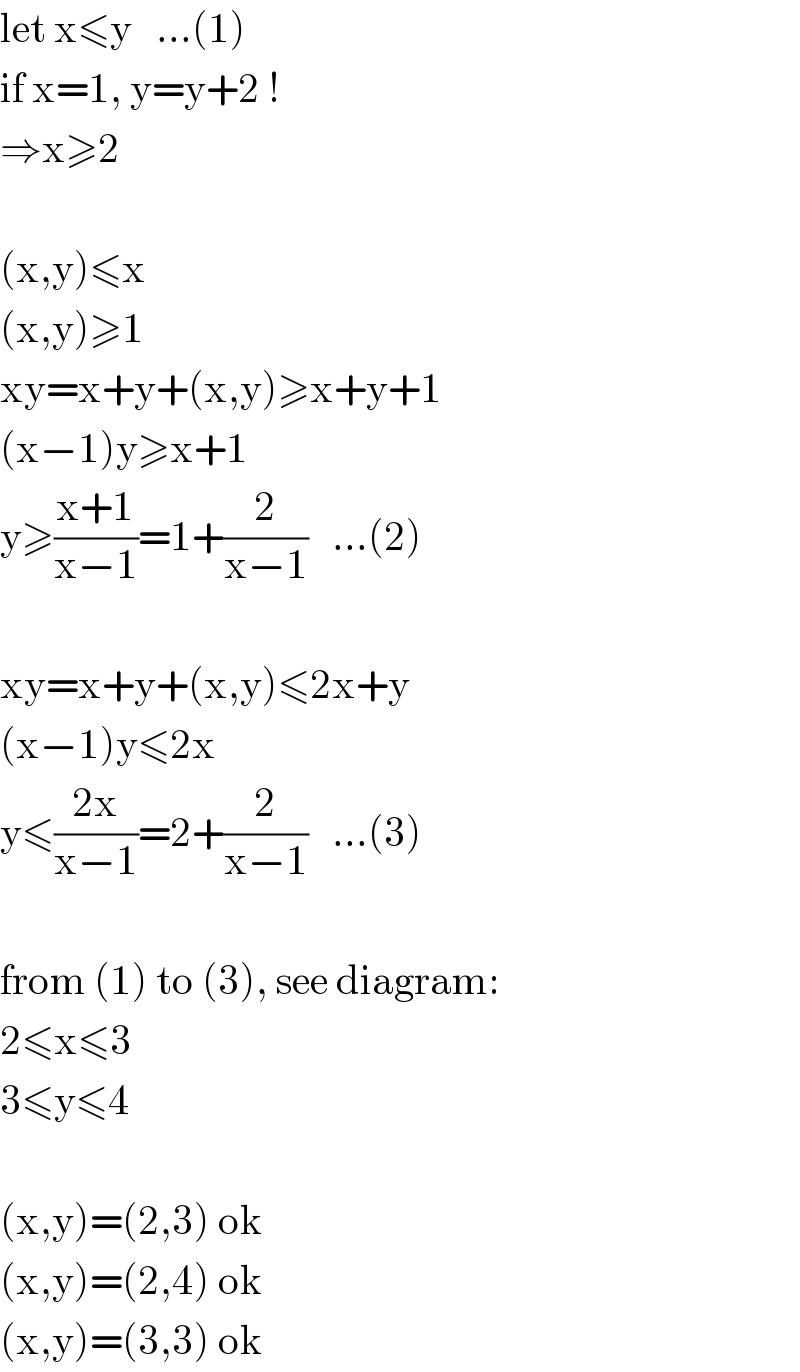
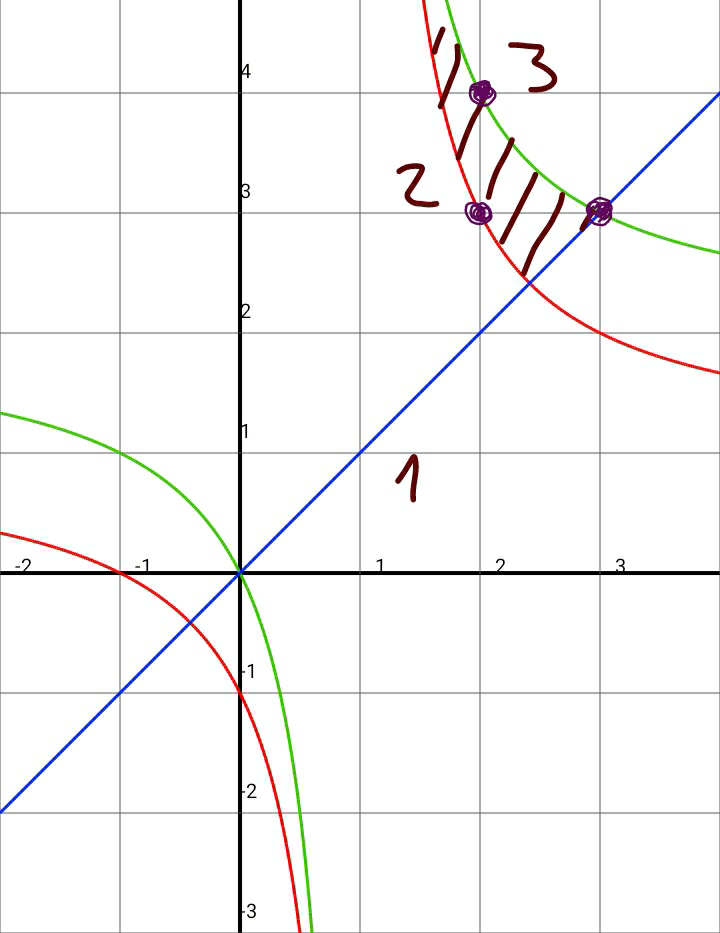
$$\mathrm{let}\mathrm{x}⩽\mathrm{y}\dots \left(1\right)$$$$\mathrm{if}\mathrm{x}=1,\mathrm{y}=\mathrm{y}+2!$$$$\Rightarrow \mathrm{x}⩾2$$$$$$$$(\mathrm{x},\mathrm{y})⩽\mathrm{x}$$$$(\mathrm{x},\mathrm{y})⩾1$$$$\mathrm{xy}=\mathrm{x}+\mathrm{y}+(\mathrm{x},\mathrm{y})⩾\mathrm{x}+\mathrm{y}+1$$$$(\mathrm{x}-1)\mathrm{y}⩾\mathrm{x}+1$$$$\mathrm{y}⩾\frac{\mathrm{x}+1}{\mathrm{x}-1}=1+\frac{2}{\mathrm{x}-1}\dots \left(2\right)$$$$$$$$\mathrm{xy}=\mathrm{x}+\mathrm{y}+(\mathrm{x},\mathrm{y})⩽2\mathrm{x}+\mathrm{y}$$$$(\mathrm{x}-1)\mathrm{y}⩽2\mathrm{x}$$$$\mathrm{y}⩽\frac{2\mathrm{x}}{\mathrm{x}-1}=2+\frac{2}{\mathrm{x}-1}\dots \left(3\right)$$$$$$$$\mathrm{from}\left(1\right)\mathrm{to}\left(3\right),\mathrm{see}\mathrm{diagram}:$$$$2⩽\mathrm{x}⩽3$$$$3⩽\mathrm{y}⩽4$$$$$$$$(\mathrm{x},\mathrm{y})=(2,3)\mathrm{ok}$$$$(\mathrm{x},\mathrm{y})=(2,4)\mathrm{ok}$$$$(\mathrm{x},\mathrm{y})=(3,3)\mathrm{ok}$$

Commented by mrW1 last updated on 16/Aug/17

$$\mathrm{y}⩾1+\frac{2}{\mathrm{x}-1}⩾1+\frac{2}{\mathrm{y}-1}$$$${(\mathrm{y}-1)}^2⩾2$$$$\Rightarrow \mathrm{y}⩾1+\sqrt{2}\approx 2.41$$$$$$$$\mathrm{y}⩽2+\frac{2}{\mathrm{x}-1}$$$$2⩾(\mathrm{y}-2)(\mathrm{x}-1)⩾(\mathrm{x}-2)(\mathrm{x}-1)={\mathrm{x}}^2-3\mathrm{x}+2$$$${\mathrm{x}}^2-3\mathrm{x}+2⩽2$$$$\mathrm{x}(\mathrm{x}-3)⩽0$$$$\Rightarrow \mathrm{x}⩽3$$$$$$$$\Rightarrow 2⩽\mathrm{x}⩽3$$

Commented by mrW1 last updated on 16/Aug/17

Commented by Tinkutara last updated on 16/Aug/17

$${\mathrm{Can}}^{\prime }\mathrm{t}\mathrm{it}\mathrm{be}\mathrm{solved}\mathrm{without}\mathrm{diagram}?$$$$\mathrm{We}\mathrm{have}\mathrm{to}\mathrm{prove}x⩽3.\mathrm{Can}\mathrm{we},\mathrm{in}$$$$\mathrm{this}\mathrm{question},\mathrm{do}\mathrm{this}?$$

Commented by Tinkutara last updated on 16/Aug/17

$$\mathrm{Thank}\mathrm{you}\mathrm{very}\mathrm{much}\mathrm{Sir}!$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin