Question Number 43792 by gunawan last updated on 15/Sep/18
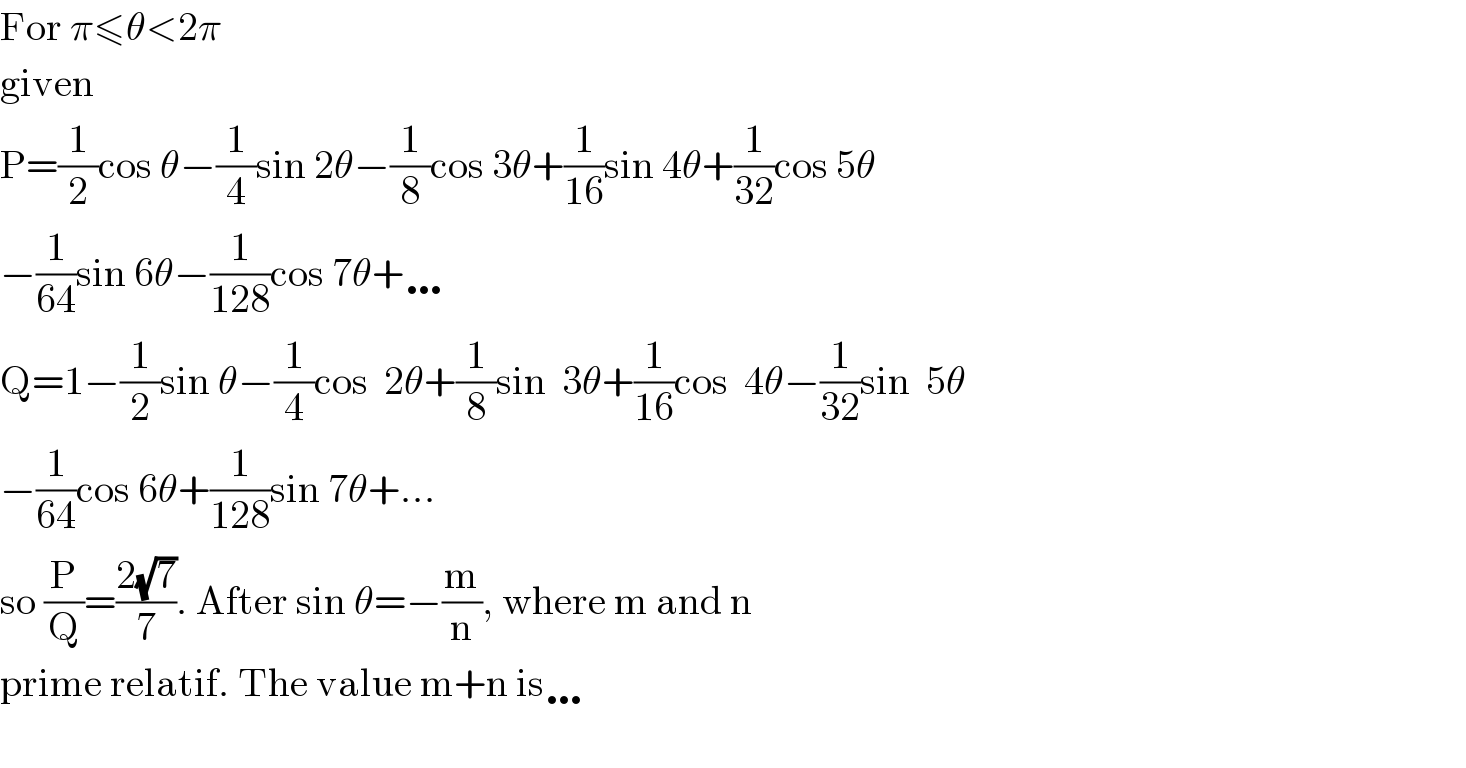
$$\mathrm{For}\:\pi\leqslant\theta<\mathrm{2}\pi \\ $$$$\mathrm{given}\: \\ $$$$\mathrm{P}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}\theta−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\:\mathrm{3}\theta+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin}\:\mathrm{4}\theta+\frac{\mathrm{1}}{\mathrm{32}}\mathrm{cos}\:\mathrm{5}\theta \\ $$$$−\frac{\mathrm{1}}{\mathrm{64}}\mathrm{sin}\:\mathrm{6}\theta−\frac{\mathrm{1}}{\mathrm{128}}\mathrm{cos}\:\mathrm{7}\theta+\ldots \\ $$$$\mathrm{Q}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\theta−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\:\mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:\:\mathrm{3}\theta+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{cos}\:\:\mathrm{4}\theta−\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin}\:\:\mathrm{5}\theta \\ $$$$−\frac{\mathrm{1}}{\mathrm{64}}\mathrm{cos}\:\mathrm{6}\theta+\frac{\mathrm{1}}{\mathrm{128}}\mathrm{sin}\:\mathrm{7}\theta+… \\ $$$$\mathrm{so}\:\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{7}}.\:\mathrm{After}\:\mathrm{sin}\:\theta=−\frac{\mathrm{m}}{\mathrm{n}},\:\mathrm{where}\:\mathrm{m}\:\mathrm{and}\:\mathrm{n} \\ $$$$\mathrm{prime}\:\mathrm{relatif}.\:\mathrm{The}\:\mathrm{value}\:\mathrm{m}+\mathrm{n}\:\mathrm{is}\ldots \\ $$$$ \\ $$
