Menu Close

For-what-value-of-a-and-b-is-the-following-equation-true-lim-x-0-sin-2x-x-3-a-b-x-2-0-

Tinku Tara 0 Comments
Pin




Question Number 130596 by bramlexs22 last updated on 27/Jan/21
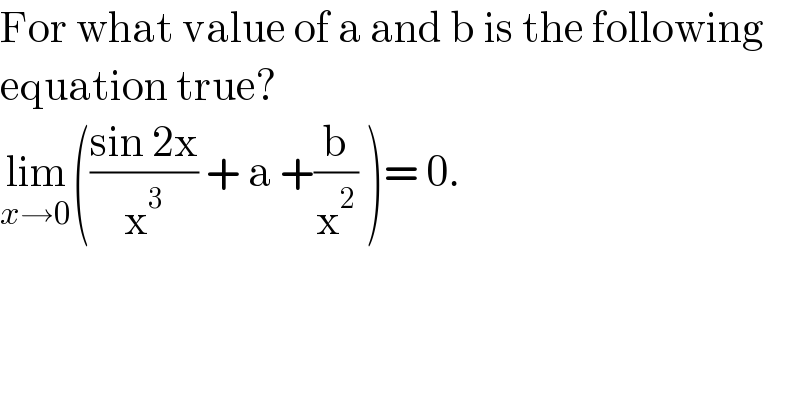
For what value of a and b is the following equation true? lim_(x→0) (((sin 2x)/x^3 ) + a +(b/x^2 ) )= 0.
$$\mathrm{For}\:\mathrm{what}\:\mathrm{value}\:\mathrm{of}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\mathrm{is}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{equation}\:\mathrm{true}?\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{x}^{\mathrm{3}} }\:+\:\mathrm{a}\:+\frac{\mathrm{b}}{\mathrm{x}^{\mathrm{2}} }\:\right)=\:\mathrm{0}. \\ $$
Answered by mr W last updated on 27/Jan/21
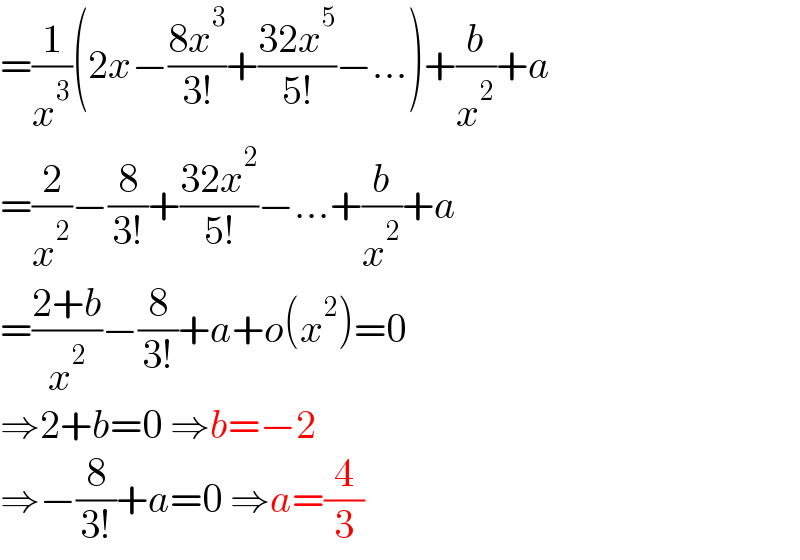
=(1/x^3 )(2x−((8x^3 )/(3!))+((32x^5 )/(5!))−...)+(b/x^2 )+a =(2/x^2 )−(8/(3!))+((32x^2 )/(5!))−...+(b/x^2 )+a =((2+b)/x^2 )−(8/(3!))+a+o(x^2 )=0 ⇒2+b=0 ⇒b=−2 ⇒−(8/(3!))+a=0 ⇒a=(4/3)
$$=\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\left(\mathrm{2}{x}−\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{32}{x}^{\mathrm{5}} }{\mathrm{5}!}−…\right)+\frac{{b}}{{x}^{\mathrm{2}} }+{a} \\ $$$$=\frac{\mathrm{2}}{{x}^{\mathrm{2}} }−\frac{\mathrm{8}}{\mathrm{3}!}+\frac{\mathrm{32}{x}^{\mathrm{2}} }{\mathrm{5}!}−…+\frac{{b}}{{x}^{\mathrm{2}} }+{a} \\ $$$$=\frac{\mathrm{2}+{b}}{{x}^{\mathrm{2}} }−\frac{\mathrm{8}}{\mathrm{3}!}+{a}+{o}\left({x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}+{b}=\mathrm{0}\:\Rightarrow{b}=−\mathrm{2} \\ $$$$\Rightarrow−\frac{\mathrm{8}}{\mathrm{3}!}+{a}=\mathrm{0}\:\Rightarrow{a}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Answered by EDWIN88 last updated on 27/Jan/21
lim_(x→0) (((sin 2x+ax^3 +bx)/x^3 )) = 0 denumerator x^3 =0, as x→0 by L′Ho^� pital rule lim_(x→0) (((2cos 2x+3ax^2 +b)/(3x^2 )))=0 (1) 2+b = 0 , b=−2 then lim_(x→0) (((2cos 2x+3ax^2 −2)/(3x^2 )))=0 lim_(x→0) (((2(1−2sin^2 x−1)+3ax^2 )/(3x^2 )))=0 lim_(x→0) (((−4sin^2 x+3ax^2 )/(3x^2 )))=0 ⇒((−4+3a)/3) = 0 ; a=(4/3)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{2}{x}+{ax}^{\mathrm{3}} +{bx}}{{x}^{\mathrm{3}} }\right)\:=\:\mathrm{0} \\ $$$$\:{denumerator}\:{x}^{\mathrm{3}} =\mathrm{0},\:{as}\:{x}\rightarrow\mathrm{0} \\ $$$${by}\:{L}'{H}\hat {{o}pital}\:{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2cos}\:\mathrm{2}{x}+\mathrm{3}{ax}^{\mathrm{2}} +{b}}{\mathrm{3}{x}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}+{b}\:=\:\mathrm{0}\:,\:{b}=−\mathrm{2} \\ $$$${then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2cos}\:\mathrm{2}{x}+\mathrm{3}{ax}^{\mathrm{2}} −\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}−\mathrm{1}\right)+\mathrm{3}{ax}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{4sin}\:^{\mathrm{2}} {x}+\mathrm{3}{ax}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\:\Rightarrow\frac{−\mathrm{4}+\mathrm{3}{a}}{\mathrm{3}}\:=\:\mathrm{0}\:;\:{a}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *