Question Number 31672 by gunawan last updated on 12/Mar/18
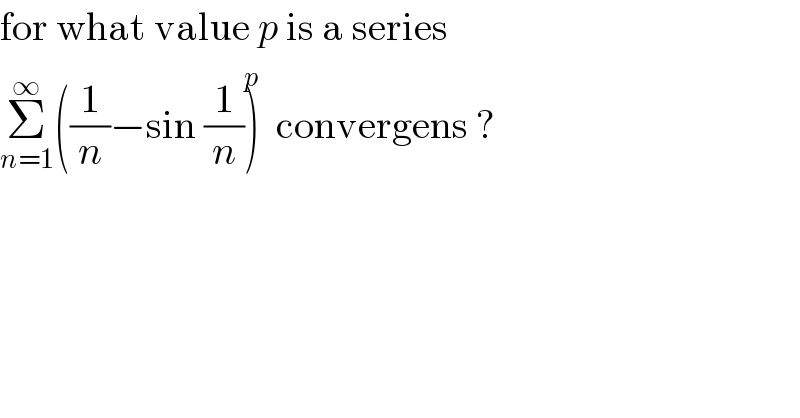
$$\mathrm{for}\:\mathrm{what}\:\mathrm{value}\:{p}\:\mathrm{is}\:\mathrm{a}\:\mathrm{series} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\mathrm{sin}\:\frac{\mathrm{1}}{{n}}\overset{{p}} {\right)}\:\:\mathrm{convergens}\:? \\ $$
Commented by abdo imad last updated on 12/Mar/18
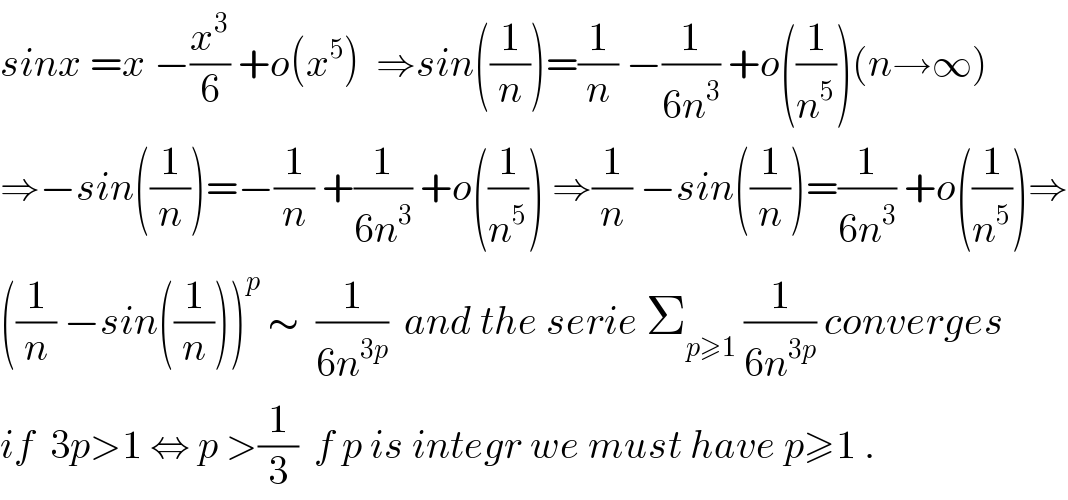
$${sinx}\:={x}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{5}} \right)\:\:\Rightarrow{sin}\left(\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{\mathrm{6}{n}^{\mathrm{3}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{5}} }\right)\left({n}\rightarrow\infty\right) \\ $$$$\Rightarrow−{sin}\left(\frac{\mathrm{1}}{{n}}\right)=−\frac{\mathrm{1}}{{n}}\:+\frac{\mathrm{1}}{\mathrm{6}{n}^{\mathrm{3}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{5}} }\right)\:\Rightarrow\frac{\mathrm{1}}{{n}}\:−{sin}\left(\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{\mathrm{6}{n}^{\mathrm{3}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{5}} }\right)\Rightarrow \\ $$$$\left(\frac{\mathrm{1}}{{n}}\:−{sin}\left(\frac{\mathrm{1}}{{n}}\right)\right)^{{p}} \:\sim\:\:\frac{\mathrm{1}}{\mathrm{6}{n}^{\mathrm{3}{p}} }\:\:{and}\:{the}\:{serie}\:\sum_{{p}\geqslant\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{6}{n}^{\mathrm{3}{p}} }\:{converges} \\ $$$${if}\:\:\mathrm{3}{p}>\mathrm{1}\:\Leftrightarrow\:{p}\:>\frac{\mathrm{1}}{\mathrm{3}}\:\:{f}\:{p}\:{is}\:{integr}\:{we}\:{must}\:{have}\:{p}\geqslant\mathrm{1}\:. \\ $$
Commented by gunawan last updated on 12/Mar/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
