Question Number 174672 by Best1 last updated on 08/Aug/22
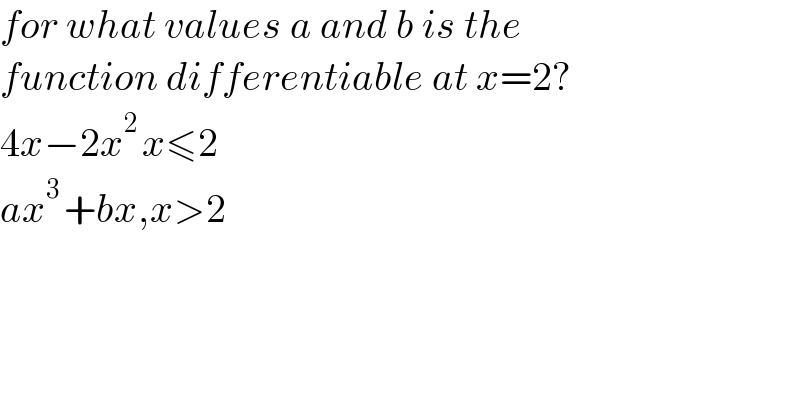
$${for}\:{what}\:{values}\:{a}\:{and}\:{b}\:{is}\:{the}\: \\ $$$${function}\:{differentiable}\:{at}\:{x}=\mathrm{2}? \\ $$$$\mathrm{4}{x}−\mathrm{2}{x}^{\mathrm{2}\:} {x}\leqslant\mathrm{2} \\ $$$${ax}^{\mathrm{3}\:} +{bx},{x}>\mathrm{2} \\ $$
Answered by MJS_new last updated on 08/Aug/22
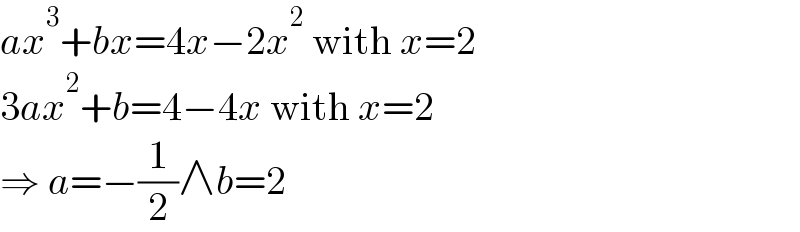
$${ax}^{\mathrm{3}} +{bx}=\mathrm{4}{x}−\mathrm{2}{x}^{\mathrm{2}} \:\mathrm{with}\:{x}=\mathrm{2} \\ $$$$\mathrm{3}{ax}^{\mathrm{2}} +{b}=\mathrm{4}−\mathrm{4}{x}\:\mathrm{with}\:{x}=\mathrm{2} \\ $$$$\Rightarrow\:{a}=−\frac{\mathrm{1}}{\mathrm{2}}\wedge{b}=\mathrm{2} \\ $$
