Question Number 13591 by FilupS last updated on 21/May/17

$$\mathrm{for}: \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as}: \\ $$$${r}=\mathrm{2sin}\left(\theta\right) \\ $$
Commented by FilupS last updated on 21/May/17

$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advanced}. \\ $$$$\mathrm{I}\:\mathrm{forgot}\:\mathrm{how}\:\mathrm{to}\:\mathrm{parameterize} \\ $$
Answered by ajfour last updated on 21/May/17
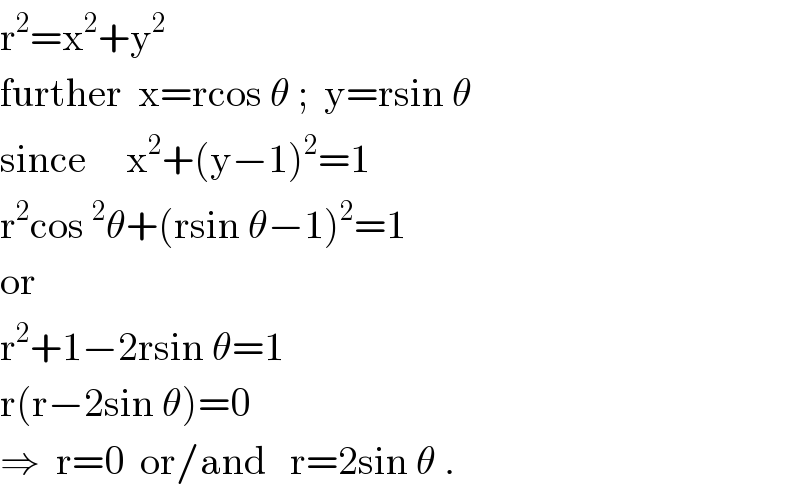
$$\mathrm{r}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{further}\:\:\mathrm{x}=\mathrm{rcos}\:\theta\:;\:\:\mathrm{y}=\mathrm{rsin}\:\theta \\ $$$$\mathrm{since}\:\:\:\:\:\mathrm{x}^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+\left(\mathrm{rsin}\:\theta−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{or} \\ $$$$\mathrm{r}^{\mathrm{2}} +\mathrm{1}−\mathrm{2rsin}\:\theta=\mathrm{1} \\ $$$$\mathrm{r}\left(\mathrm{r}−\mathrm{2sin}\:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{r}=\mathrm{0}\:\:\mathrm{or}/\mathrm{and}\:\:\:\mathrm{r}=\mathrm{2sin}\:\theta\:. \\ $$
