Question Number 83956 by jagoll last updated on 08/Mar/20

$$\mathrm{for}\:\mathrm{x}\:\in\:\mathbb{R}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{3x}\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\:\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right) \\ $$$$\mathrm{find}\:\mathrm{f}\left(\mathrm{2019}\right)\:.\: \\ $$
Commented by mr W last updated on 08/Mar/20

$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{3x}\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\:\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)\:\:\:…\left({i}\right) \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{{x}}\right)+\frac{\mathrm{3}}{{x}}\:\mathrm{f}\left({x}\right)\:=\:\mathrm{2}\left(\frac{\mathrm{1}+{x}}{{x}}\right)\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)−\mathrm{3}{x}\left({ii}\right): \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}+{x}}{\mathrm{2}} \\ $$$$\Rightarrow{f}\left(\mathrm{2019}\right)=\frac{\mathrm{1}+\mathrm{2019}}{\mathrm{2}}=\mathrm{1010} \\ $$
Answered by john santu last updated on 08/Mar/20
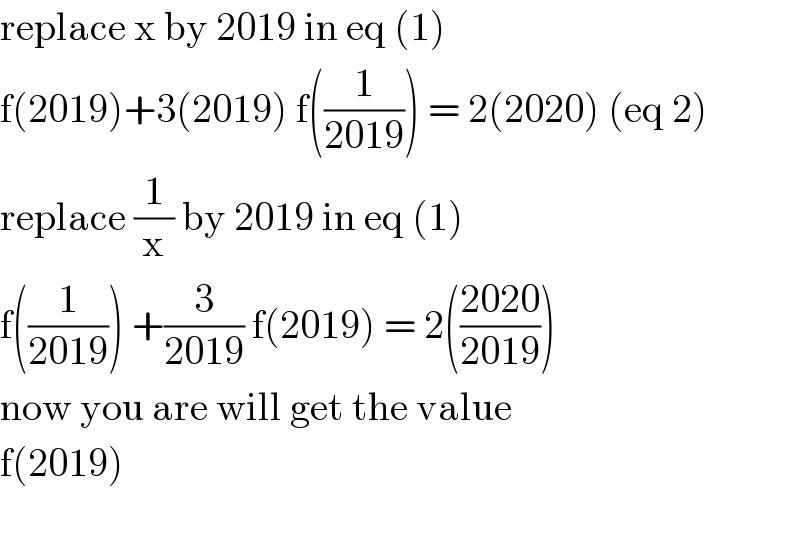
$$\mathrm{replace}\:\mathrm{x}\:\mathrm{by}\:\mathrm{2019}\:\mathrm{in}\:\mathrm{eq}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{2019}\right)+\mathrm{3}\left(\mathrm{2019}\right)\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2019}}\right)\:=\:\mathrm{2}\left(\mathrm{2020}\right)\:\left(\mathrm{eq}\:\mathrm{2}\right) \\ $$$$\mathrm{replace}\:\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{by}\:\mathrm{2019}\:\mathrm{in}\:\mathrm{eq}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2019}}\right)\:+\frac{\mathrm{3}}{\mathrm{2019}}\:\mathrm{f}\left(\mathrm{2019}\right)\:=\:\mathrm{2}\left(\frac{\mathrm{2020}}{\mathrm{2019}}\right) \\ $$$$\mathrm{now}\:\mathrm{you}\:\mathrm{are}\:\mathrm{will}\:\mathrm{get}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{f}\left(\mathrm{2019}\right)\: \\ $$$$ \\ $$
