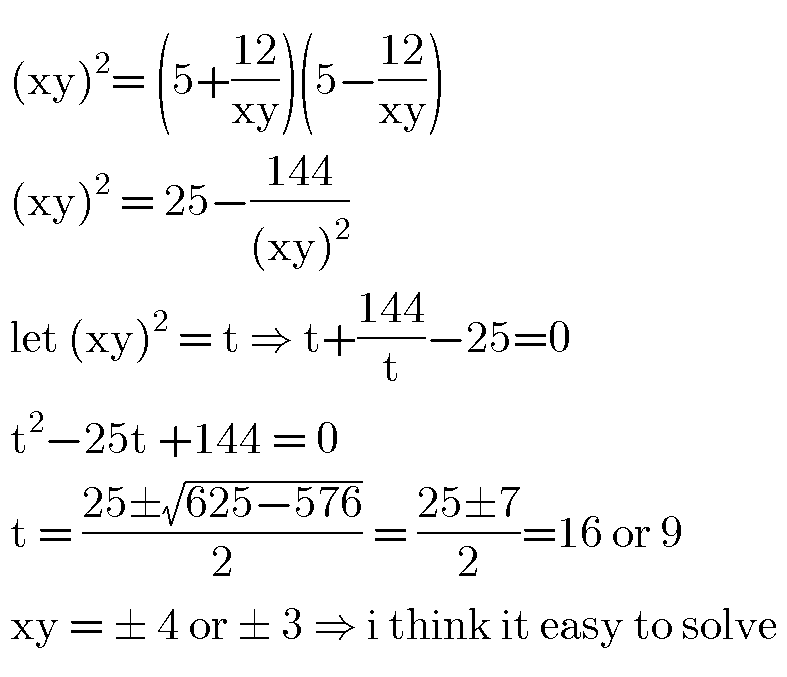for-x-y-R-x-y-gt-0-satisfy-the-equation-x-3-y-xy-3-24-x-2-y-2-10-find-the-possible-value-of-x-y-a-6-b-5-c-4-d-3-2-e-2-

Question Number 87561 by jagoll last updated on 05/Apr/20

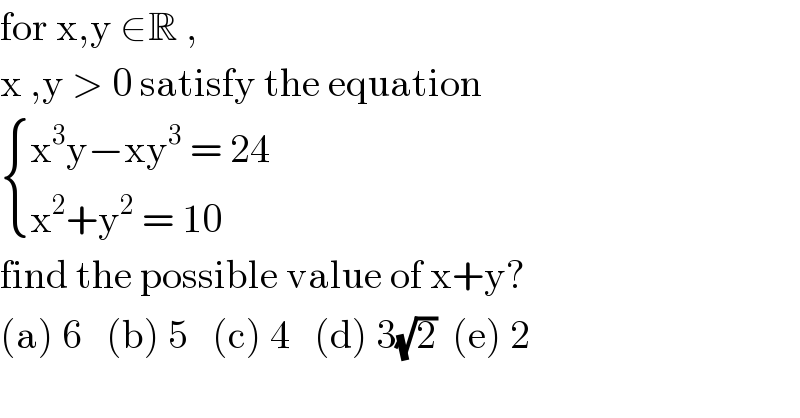
for x,y ∈R , x ,y > 0 satisfy the equation { ((x^3 y−xy^3 = 24)),((x^2 +y^2 = 10 )) :} find the possible value of x+y? (a) 6 (b) 5 (c) 4 (d) 3(√2) (e) 2

$$\mathrm{for}\:\mathrm{x},\mathrm{y}\:\in\mathbb{R}\:,\: \\ $$$$\mathrm{x}\:,\mathrm{y}\:>\:\mathrm{0}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{3}} \mathrm{y}−\mathrm{xy}^{\mathrm{3}} \:=\:\mathrm{24}}\\{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{10}\:}\end{cases} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}+\mathrm{y}? \\ $$$$\left(\mathrm{a}\right)\:\mathrm{6}\:\:\:\left(\mathrm{b}\right)\:\mathrm{5}\:\:\:\left(\mathrm{c}\right)\:\mathrm{4}\:\:\:\left(\mathrm{d}\right)\:\mathrm{3}\sqrt{\mathrm{2}}\:\:\left(\mathrm{e}\right)\:\mathrm{2} \\ $$

Commented by danger last updated on 05/Apr/20