Question Number 175799 by cortano1 last updated on 07/Sep/22
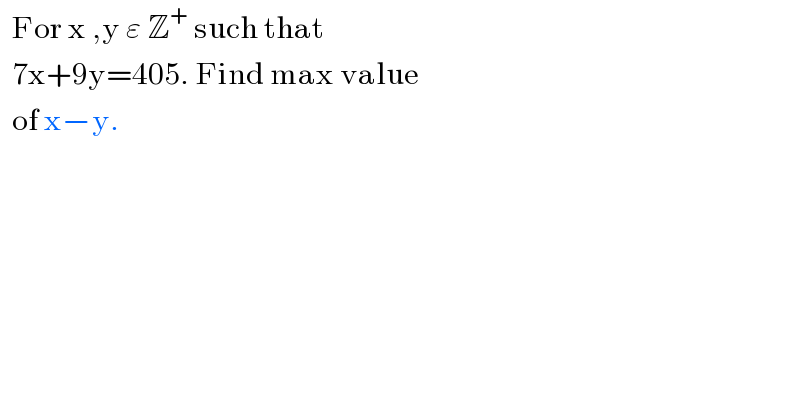
$$\:\:\mathrm{For}\:\mathrm{x}\:,\mathrm{y}\:\varepsilon\:\mathbb{Z}^{+} \:\mathrm{such}\:\mathrm{that}\: \\ $$$$\:\:\mathrm{7x}+\mathrm{9y}=\mathrm{405}.\:\mathrm{Find}\:\mathrm{max}\:\mathrm{value} \\ $$$$\:\:\mathrm{of}\:\mathrm{x}−\mathrm{y}. \\ $$
Answered by mr W last updated on 07/Sep/22
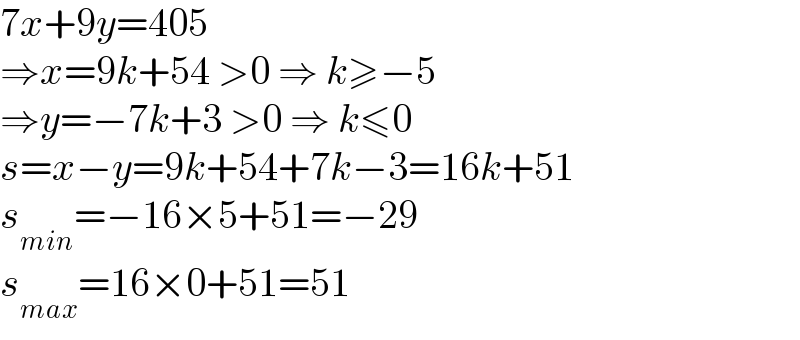
$$\mathrm{7}{x}+\mathrm{9}{y}=\mathrm{405} \\ $$$$\Rightarrow{x}=\mathrm{9}{k}+\mathrm{54}\:>\mathrm{0}\:\Rightarrow\:{k}\geqslant−\mathrm{5} \\ $$$$\Rightarrow{y}=−\mathrm{7}{k}+\mathrm{3}\:>\mathrm{0}\:\Rightarrow\:{k}\leqslant\mathrm{0} \\ $$$${s}={x}−{y}=\mathrm{9}{k}+\mathrm{54}+\mathrm{7}{k}−\mathrm{3}=\mathrm{16}{k}+\mathrm{51} \\ $$$${s}_{{min}} =−\mathrm{16}×\mathrm{5}+\mathrm{51}=−\mathrm{29} \\ $$$${s}_{{max}} =\mathrm{16}×\mathrm{0}+\mathrm{51}=\mathrm{51} \\ $$
Commented by cortano1 last updated on 07/Sep/22

$$\mathrm{nice} \\ $$
Answered by blackmamba last updated on 07/Sep/22
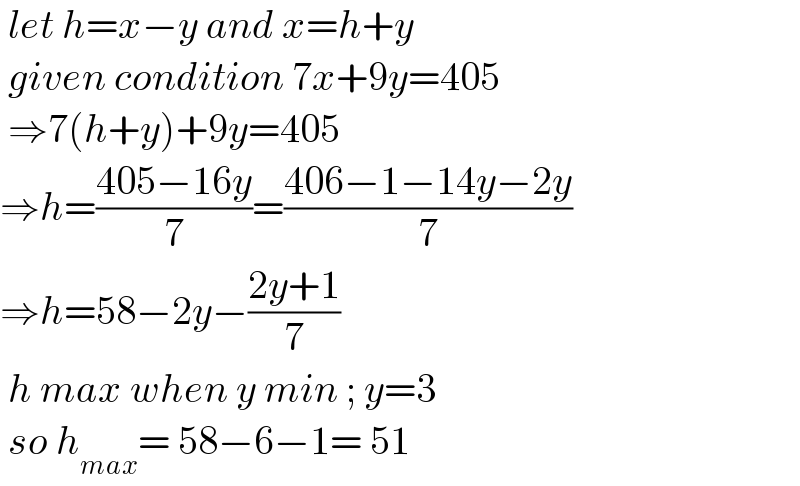
$$\:{let}\:{h}={x}−{y}\:{and}\:{x}={h}+{y} \\ $$$$\:{given}\:{condition}\:\mathrm{7}{x}+\mathrm{9}{y}=\mathrm{405} \\ $$$$\:\Rightarrow\mathrm{7}\left({h}+{y}\right)+\mathrm{9}{y}=\mathrm{405} \\ $$$$\Rightarrow{h}=\frac{\mathrm{405}−\mathrm{16}{y}}{\mathrm{7}}=\frac{\mathrm{406}−\mathrm{1}−\mathrm{14}{y}−\mathrm{2}{y}}{\mathrm{7}} \\ $$$$\Rightarrow{h}=\mathrm{58}−\mathrm{2}{y}−\frac{\mathrm{2}{y}+\mathrm{1}}{\mathrm{7}} \\ $$$$\:{h}\:{max}\:{when}\:{y}\:{min}\:;\:{y}=\mathrm{3} \\ $$$$\:{so}\:{h}_{{max}} =\:\mathrm{58}−\mathrm{6}−\mathrm{1}=\:\mathrm{51} \\ $$
