Menu Close

for-z-1-1-show-that-tan-arg-z-1-2-2i-z-1-

Tinku Tara 0 Comments
Pin




Question Number 87302 by M±th+et£s last updated on 03/Apr/20
for ∣z−1∣=1 show that tan(((arg(z−1))/2))−((2i)/z)=−1
$${for}\:\mid{z}−\mathrm{1}\mid=\mathrm{1}\:{show}\:{that} \\ $$$${tan}\left(\frac{{arg}\left({z}−\mathrm{1}\right)}{\mathrm{2}}\right)−\frac{\mathrm{2}{i}}{{z}}=−\mathrm{1} \\ $$
Commented by MJS last updated on 04/Apr/20
tan ((arg (z−1))/2) ∈R −((2i)/z)∉R ∀ z=a+bi; a≠0 ⇒ generally lhs∉R but rhs=−1∈R the equation is wrong ∣z−1∣=1 is a circle: z=a+bi ∣a−1+bi∣=1 ⇔ (√((a−1)^2 +b^2 ))=1 ⇔ b=±(√(2a−a^2 )) ⇒ generally z=a+bi; a≠0
$$\mathrm{tan}\:\frac{\mathrm{arg}\:\left({z}−\mathrm{1}\right)}{\mathrm{2}}\:\in\mathbb{R} \\ $$$$−\frac{\mathrm{2i}}{{z}}\notin\mathbb{R}\:\forall\:{z}={a}+{b}\mathrm{i};\:{a}\neq\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{generally}\:\mathrm{lhs}\notin\mathbb{R}\:\mathrm{but}\:\mathrm{rhs}=−\mathrm{1}\in\mathbb{R}\:\mathrm{the} \\ $$$$\:\:\:\:\:\mathrm{equation}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$ \\ $$$$\mid{z}−\mathrm{1}\mid=\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle}: \\ $$$${z}={a}+{b}\mathrm{i} \\ $$$$\mid{a}−\mathrm{1}+{b}\mathrm{i}\mid=\mathrm{1}\:\Leftrightarrow\:\sqrt{\left({a}−\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }=\mathrm{1}\:\Leftrightarrow\:{b}=\pm\sqrt{\mathrm{2}{a}−{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{generally}\:{z}={a}+{b}\mathrm{i};\:{a}\neq\mathrm{0} \\ $$
Commented by M±th+et£s last updated on 04/Apr/20
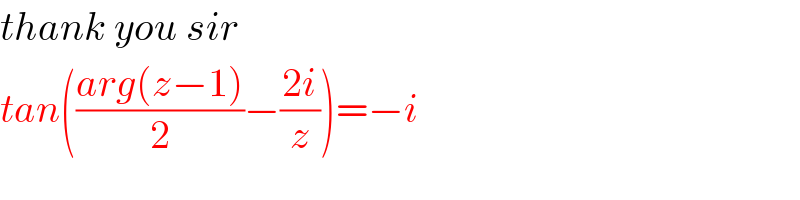
thank you sir tan(((arg(z−1))/2)−((2i)/z))=−i
$${thank}\:{you}\:{sir}\: \\ $$$${tan}\left(\frac{{arg}\left({z}−\mathrm{1}\right)}{\mathrm{2}}−\frac{\mathrm{2}{i}}{{z}}\right)=−{i}\: \\ $$
Commented by M±th+et£s last updated on 04/Apr/20
z−1=e^(iθ) z=1+cosθ+i sinθ z=2cos^2 (θ/2)+2cos(θ/2) sin(θ/2) z=2cos(θ/2)(cos(θ/2)+i sin(θ/2)) z=2 cos(θ/2) e^(i(θ/2)) ∴tan(((arg(z−1))/2)−((2i)/z)) =tan(θ/2) − (i/(cos(θ/2))) e^(−i (θ/2)) =tan(θ/2)−i(((cos(θ/2)−i sin(θ/2)))/(cos(θ/2))) =((sin(θ/2)−icos(θ/2)−sin(θ/2) )/(cos(θ/2)))=−i
$${z}−\mathrm{1}={e}^{{i}\theta} \\ $$$${z}=\mathrm{1}+{cos}\theta+{i}\:{sin}\theta \\ $$$${z}=\mathrm{2}{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\mathrm{2}{cos}\frac{\theta}{\mathrm{2}}\:{sin}\frac{\theta}{\mathrm{2}} \\ $$$${z}=\mathrm{2}{cos}\frac{\theta}{\mathrm{2}}\left({cos}\frac{\theta}{\mathrm{2}}+{i}\:{sin}\frac{\theta}{\mathrm{2}}\right) \\ $$$${z}=\mathrm{2}\:{cos}\frac{\theta}{\mathrm{2}}\:{e}^{{i}\frac{\theta}{\mathrm{2}}} \\ $$$$\therefore{tan}\left(\frac{{arg}\left({z}−\mathrm{1}\right)}{\mathrm{2}}−\frac{\mathrm{2}{i}}{{z}}\right) \\ $$$$={tan}\frac{\theta}{\mathrm{2}}\:−\:\frac{{i}}{{cos}\frac{\theta}{\mathrm{2}}}\:{e}^{−{i}\:\frac{\theta}{\mathrm{2}}} \\ $$$$={tan}\frac{\theta}{\mathrm{2}}−{i}\frac{\left({cos}\frac{\theta}{\mathrm{2}}−{i}\:{sin}\frac{\theta}{\mathrm{2}}\right)}{{cos}\frac{\theta}{\mathrm{2}}} \\ $$$$=\frac{{sin}\frac{\theta}{\mathrm{2}}−{icos}\frac{\theta}{\mathrm{2}}−{sin}\frac{\theta}{\mathrm{2}}\:}{{cos}\frac{\theta}{\mathrm{2}}}=−{i} \\ $$
Answered by MJS last updated on 04/Apr/20
let Z=z−1 ∣Z∣=1 ⇒ Z=cos θ +i sin θ tan ((arg Z)/2) =−i+((2i)/(Z+1)) tan (θ/2) =−i+((2i)/(1+cos θ +i sin θ)) tan (θ/2)=−i+((2i(1+cos θ −i sin θ))/((1+cos θ)^2 +sin^2 θ)) tan (θ/2) =−i+((2sin θ +2(1+cos θ)i)/(2+2cos θ)) tan (θ/2)=−i+((sin θ)/(1+cos θ))+i tan (θ/2) =((sin θ)/(1+cos θ)) this is a well known formula true!
$$\mathrm{let}\:{Z}={z}−\mathrm{1} \\ $$$$\mid{Z}\mid=\mathrm{1}\:\Rightarrow\:{Z}=\mathrm{cos}\:\theta\:+\mathrm{i}\:\mathrm{sin}\:\theta \\ $$$$\mathrm{tan}\:\frac{\mathrm{arg}\:{Z}}{\mathrm{2}}\:=−\mathrm{i}+\frac{\mathrm{2i}}{{Z}+\mathrm{1}} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:=−\mathrm{i}+\frac{\mathrm{2i}}{\mathrm{1}+\mathrm{cos}\:\theta\:+\mathrm{i}\:\mathrm{sin}\:\theta} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=−\mathrm{i}+\frac{\mathrm{2i}\left(\mathrm{1}+\mathrm{cos}\:\theta\:−\mathrm{i}\:\mathrm{sin}\:\theta\right)}{\left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:=−\mathrm{i}+\frac{\mathrm{2sin}\:\theta\:+\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{i}}{\mathrm{2}+\mathrm{2cos}\:\theta} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=−\mathrm{i}+\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}+\mathrm{i} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:=\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{well}\:\mathrm{known}\:\mathrm{formula} \\ $$$$\mathrm{true}! \\ $$
Commented by M±th+et£s last updated on 04/Apr/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *