Question Number 127414 by MathSh last updated on 29/Dec/20
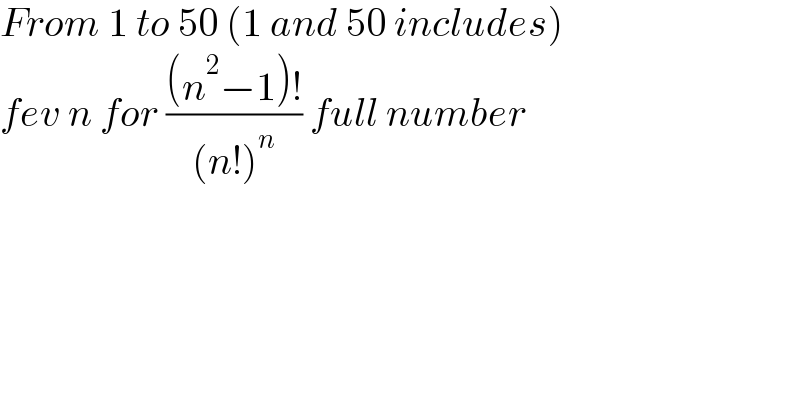
$${From}\:\mathrm{1}\:{to}\:\mathrm{50}\:\left(\mathrm{1}\:{and}\:\mathrm{50}\:{includes}\right) \\ $$$${fev}\:{n}\:{for}\:\frac{\left({n}^{\mathrm{2}} −\mathrm{1}\right)!}{\left({n}!\right)^{{n}} }\:{full}\:{number} \\ $$
Commented by talminator2856791 last updated on 29/Dec/20

$$\:\mathrm{what}\:\mathrm{is}\:\mathrm{fev}? \\ $$
Commented by MathSh last updated on 29/Dec/20
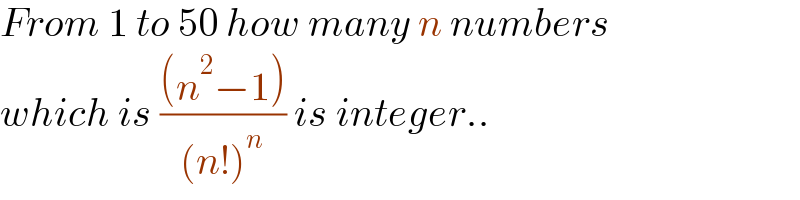
$${From}\:\mathrm{1}\:{to}\:\mathrm{50}\:{how}\:{many}\:{n}\:{numbers} \\ $$$${which}\:{is}\:\frac{\left({n}^{\mathrm{2}} −\mathrm{1}\right)}{\left({n}!\right)^{{n}} }\:{is}\:{integer}.. \\ $$
Commented by talminator2856791 last updated on 29/Dec/20

$$\:\mathrm{oooooohhhhhhh} \\ $$
Commented by MathSh last updated on 29/Dec/20
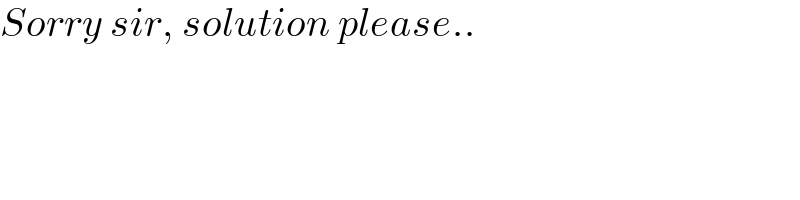
$${Sorry}\:{sir},\:{solution}\:{please}.. \\ $$
Answered by talminator2856791 last updated on 08/Sep/21
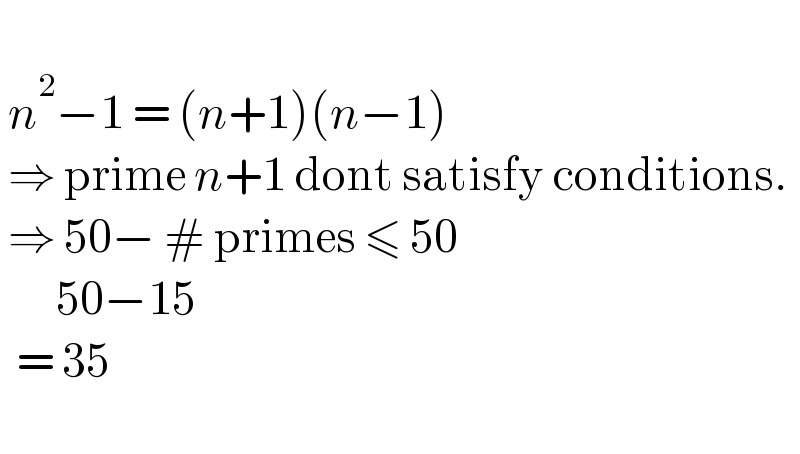
$$\: \\ $$$$\:{n}^{\mathrm{2}} −\mathrm{1}\:=\:\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right) \\ $$$$\:\Rightarrow\:\mathrm{prime}\:{n}+\mathrm{1}\:\mathrm{dont}\:\mathrm{satisfy}\:\mathrm{conditions}.\: \\ $$$$\:\Rightarrow\:\mathrm{50}−\:#\:\mathrm{primes}\:\leqslant\:\mathrm{50} \\ $$$$\:\:\:\:\:\:\:\mathrm{50}−\mathrm{15} \\ $$$$\:\:=\:\mathrm{35} \\ $$$$\: \\ $$
