Menu Close

from-sinhu-tan-prove-that-i-tanh-u-2-tan-2-ii-coshu-sec-iii-u-log-sec-tan-iv-tanhu-sin-

Tinku Tara 0 Comments
Pin




Question Number 33660 by mondodotto@gmail.com last updated on 21/Apr/18
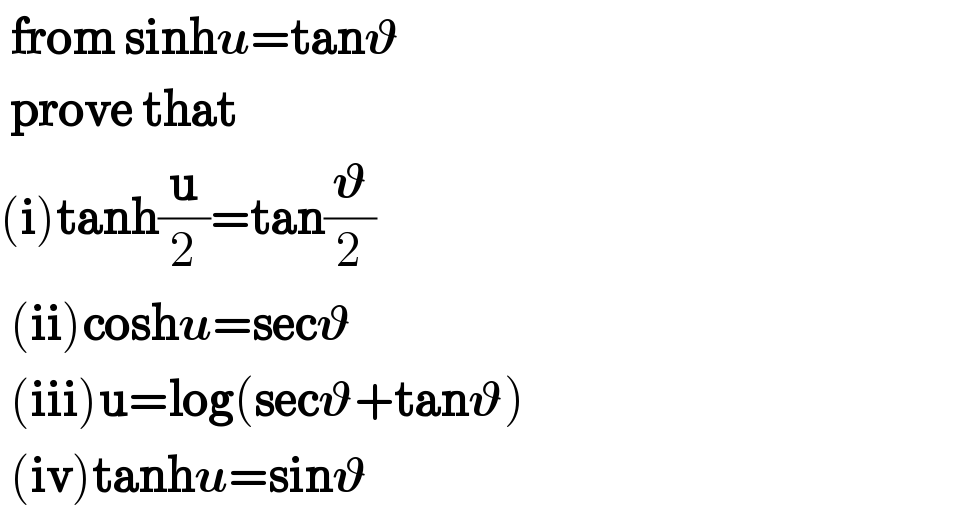
from sinhu=tan𝛝 prove that (i)tanh(u/2)=tan(𝛝/2) (ii)coshu=sec𝛝 (iii)u=log(sec𝛝+tan𝛝) (iv)tanhu=sin𝛝
$$\:\boldsymbol{\mathrm{from}}\:\boldsymbol{\mathrm{sinh}{u}}=\boldsymbol{\mathrm{tan}\vartheta} \\ $$$$\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}} \\ $$$$\left(\boldsymbol{\mathrm{i}}\right)\boldsymbol{\mathrm{tanh}}\frac{\boldsymbol{\mathrm{u}}}{\mathrm{2}}=\boldsymbol{\mathrm{tan}}\frac{\boldsymbol{\vartheta}}{\mathrm{2}} \\ $$$$\:\left(\boldsymbol{\mathrm{ii}}\right)\boldsymbol{\mathrm{cosh}{u}}=\boldsymbol{\mathrm{sec}\vartheta} \\ $$$$\:\left(\boldsymbol{\mathrm{iii}}\right)\boldsymbol{\mathrm{u}}=\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{sec}\vartheta}+\boldsymbol{\mathrm{tan}\vartheta}\right) \\ $$$$\:\left(\boldsymbol{\mathrm{iv}}\right)\boldsymbol{\mathrm{tanh}{u}}=\boldsymbol{\mathrm{sin}\vartheta} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Apr/18
sinhu=tanv (e^u βˆ’e^(βˆ’u) )/2=sinv/cosv LHS e^(u/2) +e^(βˆ’u/2) )(e^(u/2) βˆ’e^(βˆ’u/2) )/2 let a=e^(u/2) (a+1/a)(aβˆ’1/a)/2 (a^4 βˆ’1)/2a^2 RHS b=tan(v/2) 2b/1βˆ’b^2 (a^4 βˆ’1)(1βˆ’b^2 )=4a^2 b a^4 βˆ’a^4 b^2 βˆ’1+b^2 βˆ’4a^2 b=0 (a^4 βˆ’2a^2 b+b^2 )βˆ’(a^4 b^2 +2a^2 b+1)=0 (a^2 βˆ’b)^2 βˆ’(a^2 b+1)^2 =0 (a^2 βˆ’b)^2 =(a^2 b+1)^2 a^2 βˆ’b=(a^2 b+1) (a^2 βˆ’1)/(a2+1)=b (aβˆ’1/a)/(a+1/a)=b (tanh(u/2)=tan(v/2)
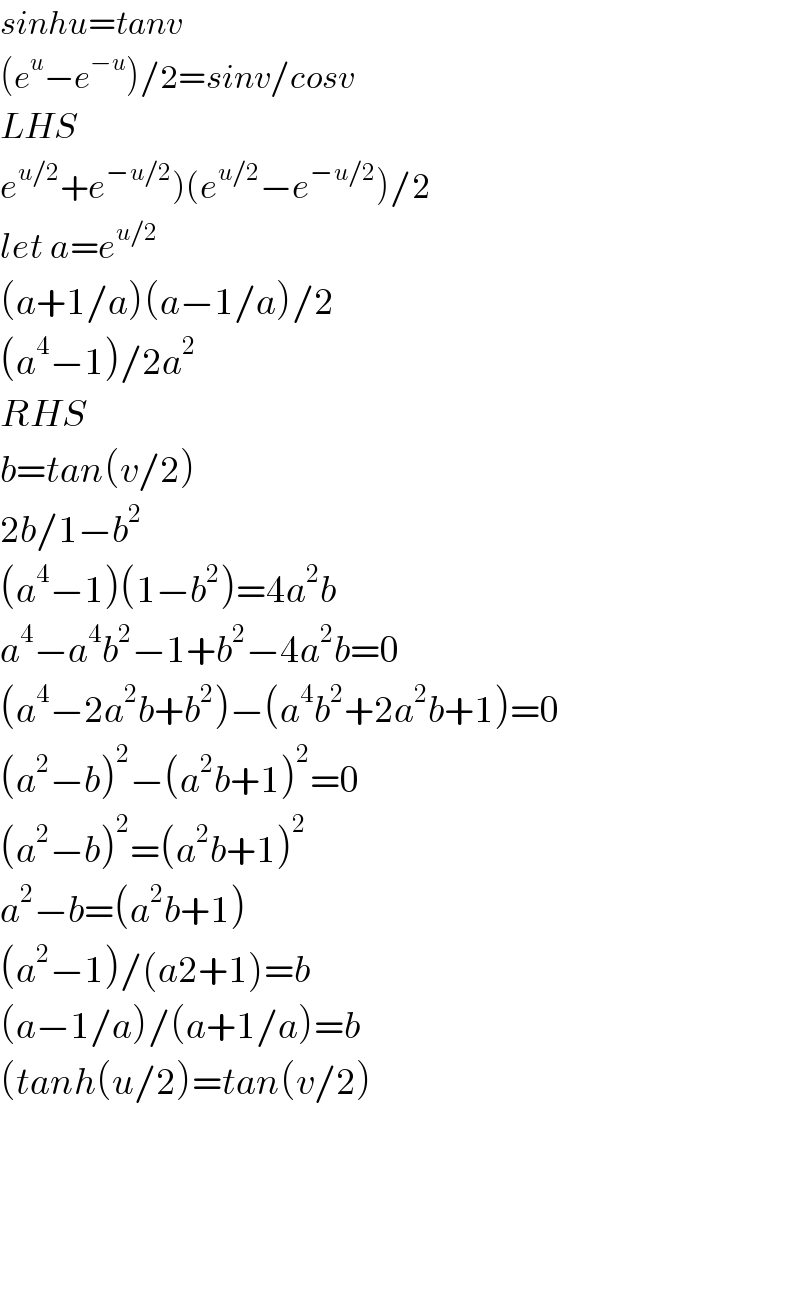
$${sinhu}={tanv} \\ $$$$\left({e}^{{u}} βˆ’{e}^{βˆ’{u}} \right)/\mathrm{2}={sinv}/{cosv} \\ $$$${LHS} \\ $$$$\left.{e}^{{u}/\mathrm{2}} +{e}^{βˆ’{u}/\mathrm{2}} \right)\left({e}^{{u}/\mathrm{2}} βˆ’{e}^{βˆ’{u}/\mathrm{2}} \right)/\mathrm{2} \\ $$$${let}\:{a}={e}^{{u}/\mathrm{2}} \\ $$$$\left({a}+\mathrm{1}/{a}\right)\left({a}βˆ’\mathrm{1}/{a}\right)/\mathrm{2} \\ $$$$\left({a}^{\mathrm{4}} βˆ’\mathrm{1}\right)/\mathrm{2}{a}^{\mathrm{2}} \\ $$$${RHS} \\ $$$${b}={tan}\left({v}/\mathrm{2}\right) \\ $$$$\mathrm{2}{b}/\mathrm{1}βˆ’{b}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{4}} βˆ’\mathrm{1}\right)\left(\mathrm{1}βˆ’{b}^{\mathrm{2}} \right)=\mathrm{4}{a}^{\mathrm{2}} {b} \\ $$$${a}^{\mathrm{4}} βˆ’{a}^{\mathrm{4}} {b}^{\mathrm{2}} βˆ’\mathrm{1}+{b}^{\mathrm{2}} βˆ’\mathrm{4}{a}^{\mathrm{2}} {b}=\mathrm{0} \\ $$$$\left({a}^{\mathrm{4}} βˆ’\mathrm{2}{a}^{\mathrm{2}} {b}+{b}^{\mathrm{2}} \right)βˆ’\left({a}^{\mathrm{4}} {b}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {b}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} βˆ’{b}\right)^{\mathrm{2}} βˆ’\left({a}^{\mathrm{2}} {b}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} βˆ’{b}\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} {b}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} βˆ’{b}=\left({a}^{\mathrm{2}} {b}+\mathrm{1}\right) \\ $$$$\left({a}^{\mathrm{2}} βˆ’\mathrm{1}\right)/\left({a}\mathrm{2}+\mathrm{1}\right)={b} \\ $$$$\left({a}βˆ’\mathrm{1}/{a}\right)/\left({a}+\mathrm{1}/{a}\right)={b} \\ $$$$\left({tanh}\left({u}/\mathrm{2}\right)={tan}\left({v}/\mathrm{2}\right)\right. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mondodotto@gmail.com last updated on 22/Apr/18
why e^(u/2) +e^((βˆ’2)/u) more explainations please
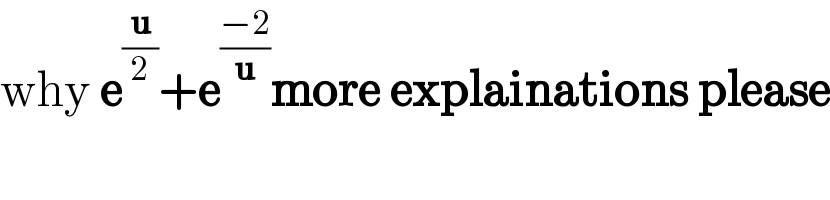
$$\mathrm{why}\:\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{\mathrm{u}}}{\mathrm{2}}} +\boldsymbol{\mathrm{e}}^{\frac{βˆ’\mathrm{2}}{\boldsymbol{\mathrm{u}}}} \boldsymbol{\mathrm{more}}\:\boldsymbol{\mathrm{explainations}}\:\boldsymbol{\mathrm{please}} \\ $$
Answered by math1967 last updated on 22/Apr/18
ii) coshu=(√(1+sinh^2 u)) β‡’coshu=(√(1+tan^2 v )) [given sinhu=tanv] ∴coshu=secv
$$\left.{ii}\right)\:{coshu}=\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {u}}\: \\ $$$$\Rightarrow{coshu}=\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {v}\:}\:\:\:\:\left[{given}\:\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{sinhu}={tanv}\right] \\ $$$$\therefore{coshu}={secv} \\ $$
Answered by math1967 last updated on 22/Apr/18
iii) sinhu+coshu=tanv +secv β‡’((e^u βˆ’e^(βˆ’u) )/2) +((e^u +e^(βˆ’u) )/2) =tanv +secv β‡’((2e^u )/2)=tanv +secv β‡’e^u =tanv +secv β‡’u=log_e (tanv +secv)
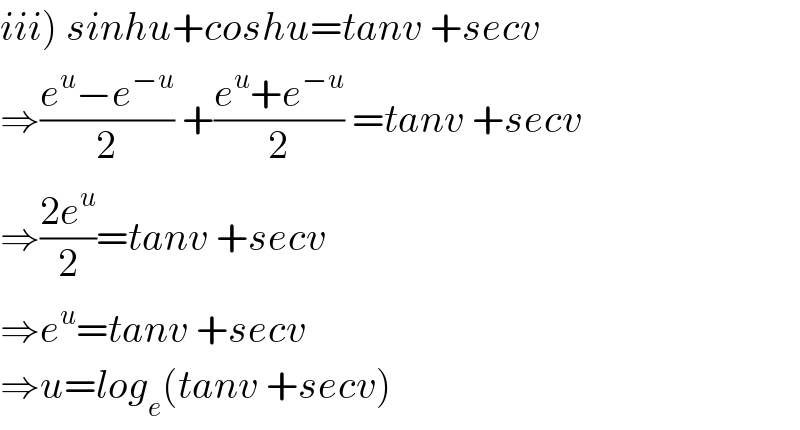
$$\left.{iii}\right)\:{sinhu}+{coshu}={tanv}\:+{secv} \\ $$$$\Rightarrow\frac{{e}^{{u}} βˆ’{e}^{βˆ’{u}} }{\mathrm{2}}\:+\frac{{e}^{{u}} +{e}^{βˆ’{u}} }{\mathrm{2}}\:={tanv}\:+{secv} \\ $$$$\Rightarrow\frac{\mathrm{2}{e}^{{u}} }{\mathrm{2}}={tanv}\:+{secv} \\ $$$$\Rightarrow{e}^{{u}} ={tanv}\:+{secv} \\ $$$$\Rightarrow{u}={log}_{{e}} \left({tanv}\:+{secv}\right) \\ $$
Answered by math1967 last updated on 22/Apr/18
iv) tanhu = ((sinhu)/(coshu)) =((tanv)/(secv)) =((sinv)/(cosvsecv))=sinv
$$\left.{iv}\right)\:{tanhu} \\ $$$$=\:\frac{{sinhu}}{{coshu}}\: \\ $$$$=\frac{{tanv}}{{secv}} \\ $$$$=\frac{{sinv}}{{cosvsecv}}={sinv} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *