Question Number 82056 by mathocean1 last updated on 17/Feb/20
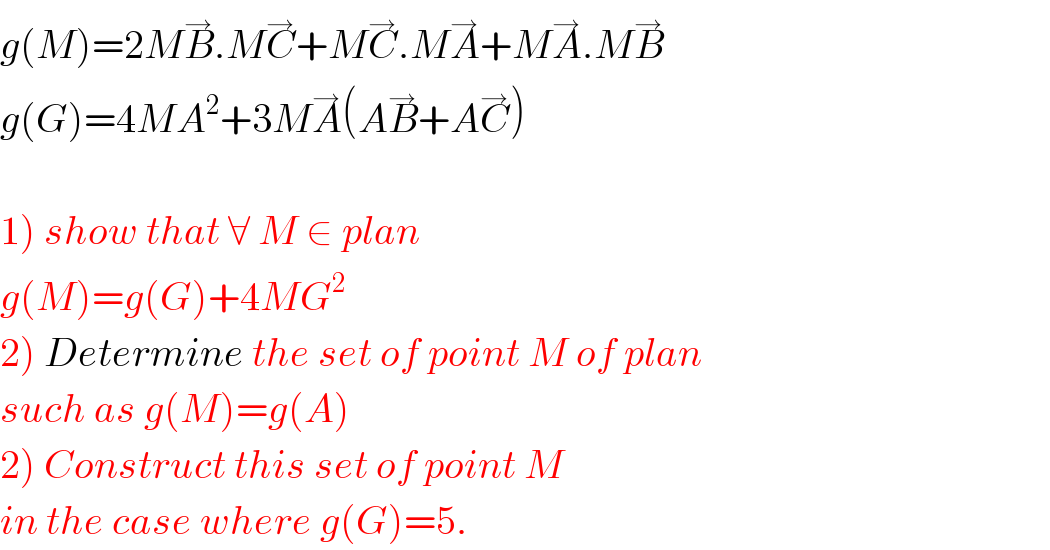
$${g}\left({M}\right)=\mathrm{2}{M}\overset{\rightarrow} {{B}}.{M}\overset{\rightarrow} {{C}}+{M}\overset{\rightarrow} {{C}}.{M}\overset{\rightarrow} {{A}}+{M}\overset{\rightarrow} {{A}}.{M}\overset{\rightarrow} {{B}} \\ $$$${g}\left({G}\right)=\mathrm{4}{MA}^{\mathrm{2}} +\mathrm{3}{M}\overset{\rightarrow} {{A}}\left({A}\overset{\rightarrow} {{B}}+{A}\overset{\rightarrow} {{C}}\right) \\ $$$$ \\ $$$$\left.\mathrm{1}\right)\:{show}\:{that}\:\forall\:{M}\:\in\:{plan} \\ $$$${g}\left({M}\right)={g}\left({G}\right)+\mathrm{4}{MG}^{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:{Determine}\:{the}\:{set}\:{of}\:{point}\:{M}\:{of}\:{plan} \\ $$$${such}\:{as}\:{g}\left({M}\right)={g}\left({A}\right) \\ $$$$\left.\mathrm{2}\right)\:{Construct}\:{this}\:{set}\:{of}\:{point}\:{M} \\ $$$${in}\:{the}\:{case}\:{where}\:{g}\left({G}\right)=\mathrm{5}. \\ $$
