Question Number 122704 by mnjuly1970 last updated on 19/Nov/20
![... general calculus... i: (1/( (√(1−4x)))) =^(??) Σ_(n=0 ) ^∞ [ (((2n)),(( n)) ) x^n ] ii: (π/2) =^? Σ_(n=0) ^∞ [( (((2n)),(( n)) )/4^n ) (1/((2n+1)))]](https://www.tinkutara.com/question/Q122704.png)
$$\:\:\:\:\:\:\:\:\:\:\:…\:{general}\:\:{calculus}… \\ $$$$\:{i}:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}}}\:\overset{??} {=}\underset{{n}=\mathrm{0}\:} {\overset{\infty} {\sum}}\left[\begin{pmatrix}{\mathrm{2}{n}}\\{\:{n}}\end{pmatrix}\:\:{x}^{{n}} \right] \\ $$$$\:{ii}:\:\frac{\pi}{\mathrm{2}}\:\overset{?} {=}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\begin{pmatrix}{\mathrm{2}{n}}\\{\:{n}}\end{pmatrix}}{\mathrm{4}^{{n}} }\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 19/Nov/20
![(1/( (√(1−4x)))) =(1−4x)^(−(1/2)) =1+2x+(3/4)16x^2 +((15)/8)64x^3 +... = 1+2x+12x^2 +120x^3 +.. = 1+((2!)/(1!))x+((4!)/(2!))x^2 +((6!)/(3!))x^3 +..=Σ_(n=0) ^∞ [ (((2n)),(n) )x^n ]](https://www.tinkutara.com/question/Q122706.png)
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}}}\:=\left(\mathrm{1}−\mathrm{4}{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1}+\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{16}{x}^{\mathrm{2}} +\frac{\mathrm{15}}{\mathrm{8}}\mathrm{64}{x}^{\mathrm{3}} +… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{1}+\mathrm{2}{x}+\mathrm{12}{x}^{\mathrm{2}} +\mathrm{120}{x}^{\mathrm{3}} +.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}+\frac{\mathrm{2}!}{\mathrm{1}!}{x}+\frac{\mathrm{4}!}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{\mathrm{6}!}{\mathrm{3}!}{x}^{\mathrm{3}} +..=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix}{x}^{{n}} \right] \\ $$
Answered by Dwaipayan Shikari last updated on 19/Nov/20
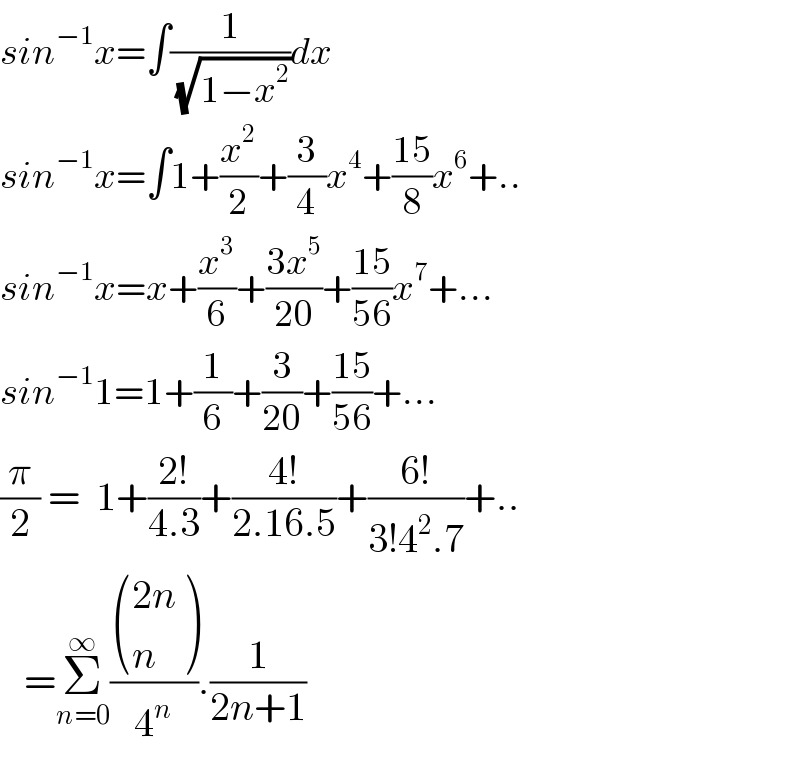
$${sin}^{−\mathrm{1}} {x}=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${sin}^{−\mathrm{1}} {x}=\int\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{4}} +\frac{\mathrm{15}}{\mathrm{8}}{x}^{\mathrm{6}} +.. \\ $$$${sin}^{−\mathrm{1}} {x}={x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{3}{x}^{\mathrm{5}} }{\mathrm{20}}+\frac{\mathrm{15}}{\mathrm{56}}{x}^{\mathrm{7}} +… \\ $$$${sin}^{−\mathrm{1}} \mathrm{1}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{20}}+\frac{\mathrm{15}}{\mathrm{56}}+… \\ $$$$\frac{\pi}{\mathrm{2}}\:=\:\:\mathrm{1}+\frac{\mathrm{2}!}{\mathrm{4}.\mathrm{3}}+\frac{\mathrm{4}!}{\mathrm{2}.\mathrm{16}.\mathrm{5}}+\frac{\mathrm{6}!}{\mathrm{3}!\mathrm{4}^{\mathrm{2}} .\mathrm{7}}+.. \\ $$$$\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix}}{\mathrm{4}^{{n}} }.\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$
Commented by mnjuly1970 last updated on 19/Nov/20
$${mercey}\:{mr}\:{payan}. \\ $$
Commented by Dwaipayan Shikari last updated on 19/Nov/20

$${With}\:{pleasure} \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 19/Nov/20
![solution ii in (i): 4x=t^2 (1/( (√(1−t^2 ))))=Σ_(n=0) ^∞ [ (((2n)),(( n)) ) (t^(2n) /4^n )] ∫_0 ^( x) (1/( (√(1−t^2 ))))dt=Σ_(n≥0) { (((2n)),(( n)) ) [(t^(2n+1) /((2n+1)4^n ))]_0 ^x } Arcsin(x)=Σ_(n=0) ^∞ (((2n)),(( n)) ) (x^(2n+1) /((2n+1)4^n )) x=1 :: (π/2) =Σ[ (((2n)),(( n)) ) (1/((2n+1)4^n )) ] ✓](https://www.tinkutara.com/question/Q122710.png)
$${solution}\:{ii} \\ $$$${in}\:\:\left({i}\right):\:\mathrm{4}{x}={t}^{\mathrm{2}} \\ $$$$\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\begin{pmatrix}{\mathrm{2}{n}}\\{\:{n}}\end{pmatrix}\:\frac{{t}^{\mathrm{2}{n}} }{\mathrm{4}^{{n}} }\right] \\ $$$$\:\:\int_{\mathrm{0}} ^{\:{x}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}=\underset{{n}\geqslant\mathrm{0}} {\sum}\left\{\begin{pmatrix}{\mathrm{2}{n}}\\{\:{n}}\end{pmatrix}\:\left[\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{4}^{{n}} }\right]_{\mathrm{0}} ^{{x}} \right\} \\ $$$$ \\ $$$$\:\:\:\:\:\:{Arcsin}\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{n}}\end{pmatrix}\:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{4}^{{n}} } \\ $$$$\:{x}=\mathrm{1}\:::\:\:\:\frac{\pi}{\mathrm{2}}\:=\Sigma\left[\begin{pmatrix}{\mathrm{2}{n}}\\{\:{n}}\end{pmatrix}\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{4}^{{n}} }\:\right]\:\checkmark \\ $$
