Question Number 149424 by mathdanisur last updated on 05/Aug/21
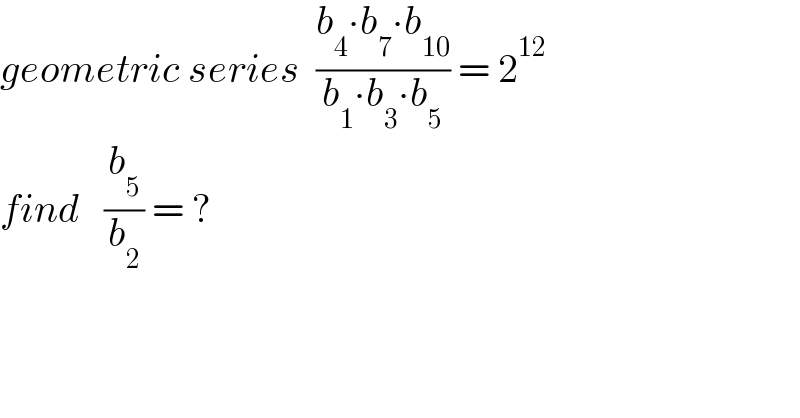
$${geometric}\:{series}\:\:\frac{{b}_{\mathrm{4}} \centerdot{b}_{\mathrm{7}} \centerdot{b}_{\mathrm{10}} }{{b}_{\mathrm{1}} \centerdot{b}_{\mathrm{3}} \centerdot{b}_{\mathrm{5}} }\:=\:\mathrm{2}^{\mathrm{12}} \\ $$$${find}\:\:\:\frac{{b}_{\mathrm{5}} }{{b}_{\mathrm{2}} }\:=\:? \\ $$
Answered by nimnim last updated on 05/Aug/21
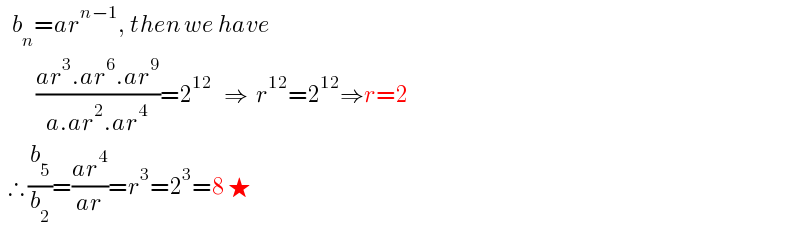
$$\:\:\:{b}_{{n}} ={ar}^{{n}−\mathrm{1}} ,\:{then}\:{we}\:{have}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{ar}^{\mathrm{3}} .{ar}^{\mathrm{6}} .{ar}^{\mathrm{9}} }{{a}.{ar}^{\mathrm{2}} .{ar}^{\mathrm{4}} }=\mathrm{2}^{\mathrm{12}} \:\:\:\Rightarrow\:\:{r}^{\mathrm{12}} =\mathrm{2}^{\mathrm{12}} \Rightarrow{r}=\mathrm{2} \\ $$$$\:\:\therefore\:\frac{{b}_{\mathrm{5}} }{{b}_{\mathrm{2}} }=\frac{{ar}^{\mathrm{4}} }{{ar}}={r}^{\mathrm{3}} =\mathrm{2}^{\mathrm{3}} =\mathrm{8}\:\bigstar \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$${Thank}\:{you}\:{Ser} \\ $$
