Question Number 112393 by ZiYangLee last updated on 07/Sep/20
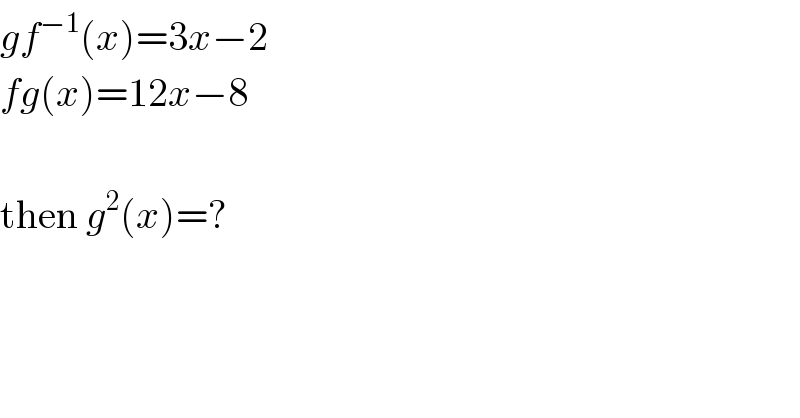
$${gf}^{−\mathrm{1}} \left({x}\right)=\mathrm{3}{x}−\mathrm{2} \\ $$$${fg}\left({x}\right)=\mathrm{12}{x}−\mathrm{8} \\ $$$$ \\ $$$$\mathrm{then}\:{g}^{\mathrm{2}} \left({x}\right)=? \\ $$
Commented by ZiYangLee last updated on 07/Sep/20

$$\mathrm{ya} \\ $$
Commented by john santu last updated on 07/Sep/20

$${gf}^{−\mathrm{1}} \:=\:{g}\left({f}^{−\mathrm{1}} \right)\:?\: \\ $$
Commented by kaivan.ahmadi last updated on 07/Sep/20
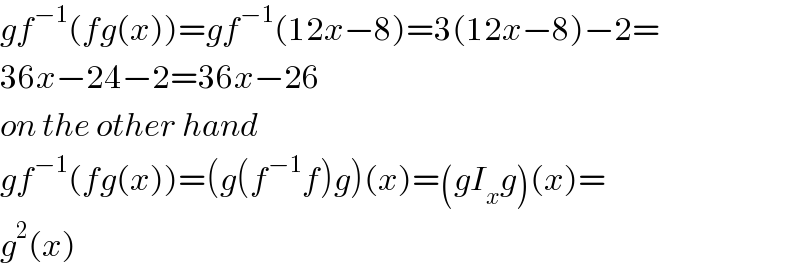
$${gf}^{−\mathrm{1}} \left({fg}\left({x}\right)\right)={gf}^{−\mathrm{1}} \left(\mathrm{12}{x}−\mathrm{8}\right)=\mathrm{3}\left(\mathrm{12}{x}−\mathrm{8}\right)−\mathrm{2}= \\ $$$$\mathrm{36}{x}−\mathrm{24}−\mathrm{2}=\mathrm{36}{x}−\mathrm{26} \\ $$$${on}\:{the}\:{other}\:{hand} \\ $$$${gf}^{−\mathrm{1}} \left({fg}\left({x}\right)\right)=\left({g}\left({f}^{−\mathrm{1}} {f}\right){g}\right)\left({x}\right)=\left({gI}_{{x}} {g}\right)\left({x}\right)= \\ $$$${g}^{\mathrm{2}} \left({x}\right) \\ $$
