Menu Close

give-at-form-of-serie-U-n-0-1-x-n-ln-x-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 98445 by mathmax by abdo last updated on 14/Jun/20
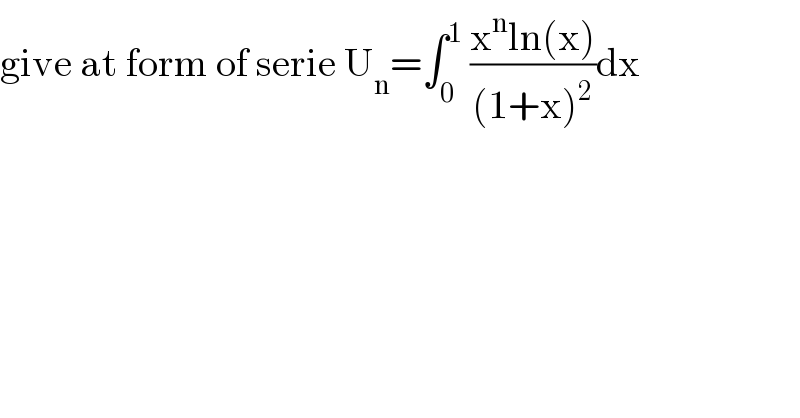
give at form of serie U_n =∫_0 ^1 ((x^n ln(x))/((1+x)^2 ))dx
$$\mathrm{give}\:\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie}\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 14/Jun/20
we have (1/(1+x)) =Σ_(k=0) ^∞ (−1)^k x^k for ∣x∣<1 ⇒ −(1/((1+x^2 ))) =Σ_(k=1) ^∞ k(−1)^k x^(k−1) =Σ_(k=0) ^∞ (k+1)(−1)^(k+1) x^k ⇒ (1/((1+x)^2 )) =Σ_(k=0) ^∞ (k+1)(−1)^k x^k ⇒U_n =∫_0 ^1 x^n ln(x)(Σ_(k=0) ^∞ (k+1)(−1)^k x^k )dx =Σ_(k=0) ^∞ (k+1)(−1)^k ∫_0 ^1 x^(n+k) ln(x)dx and by parts ∫_0 ^1 x^(n+k) ln(x)dx =[(x^(n+k+1) /(n+k+1))ln(x)]_0 ^1 −∫_0 ^1 (x^(n+k) /(n+k+1))dx =−(1/((n+k+1)^2 )) ⇒ U_n =−Σ_(k=0) ^∞ (k+1)(−1)^k ×(1/((n+k+1)^2 )) =Σ_(k=0) ^∞ ((k+1)/((n+k+1)^2 ))(−1)^(k+1) ⇒ U_n =−(1/((n+1)^2 )) +(2/((n+2)^2 ))−(3/((n+3)^2 ))+....
$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:\:\:\:\:\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\mathrm{k}\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}−\mathrm{1}} \:\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \left(\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} \:\mathrm{x}^{\mathrm{k}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\left(\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:\Rightarrow\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{x}\right)\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \left(\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\left(\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{k}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}+\mathrm{k}} \:\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:\:\:\mathrm{and}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}+\mathrm{k}} \:\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{k}+\mathrm{1}} }{\mathrm{n}+\mathrm{k}+\mathrm{1}}\mathrm{ln}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{k}} }{\mathrm{n}+\mathrm{k}+\mathrm{1}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\:\mathrm{U}_{\mathrm{n}} =−\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\left(\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{k}} ×\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{k}+\mathrm{1}}{\left(\mathrm{n}+\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{U}_{\mathrm{n}} =−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{3}}{\left(\mathrm{n}+\mathrm{3}\right)^{\mathrm{2}} }+…. \\ $$
Answered by maths mind last updated on 14/Jun/20
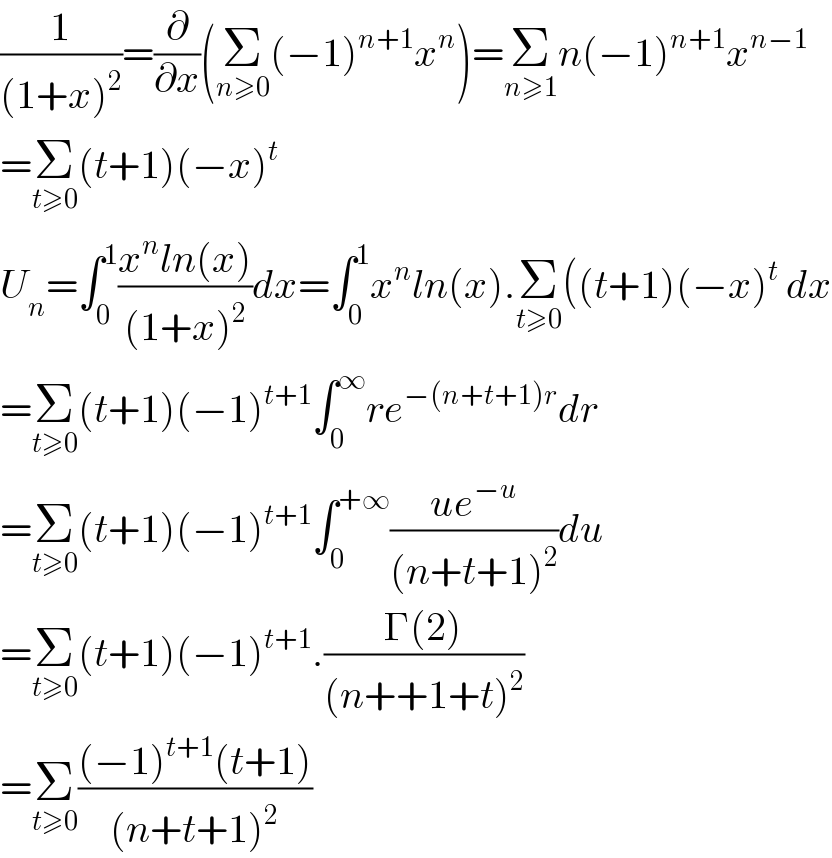
(1/((1+x)^2 ))=(∂/∂x)(Σ_(n≥0) (−1)^(n+1) x^n )=Σ_(n≥1) n(−1)^(n+1) x^(n−1) =Σ_(t≥0) (t+1)(−x)^t U_n =∫_0 ^1 ((x^n ln(x))/((1+x)^2 ))dx=∫_0 ^1 x^n ln(x).Σ_(t≥0) ((t+1)(−x)^t dx =Σ_(t≥0) (t+1)(−1)^(t+1) ∫_0 ^∞ re^(−(n+t+1)r) dr =Σ_(t≥0) (t+1)(−1)^(t+1) ∫_0 ^(+∞) ((ue^(−u) )/((n+t+1)^2 ))du =Σ_(t≥0) (t+1)(−1)^(t+1) .((Γ(2))/((n++1+t)^2 )) =Σ_(t≥0) (((−1)^(t+1) (t+1))/((n+t+1)^2 ))
$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{\partial}{\partial{x}}\left(\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}} \right)=\underset{{n}\geqslant\mathrm{1}} {\sum}{n}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}−\mathrm{1}} \\ $$$$=\underset{{t}\geqslant\mathrm{0}} {\sum}\left({t}+\mathrm{1}\right)\left(−{x}\right)^{{t}} \\ $$$${U}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} {ln}\left({x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {ln}\left({x}\right).\underset{{t}\geqslant\mathrm{0}} {\sum}\left(\left({t}+\mathrm{1}\right)\left(−{x}\right)^{{t}} \:{dx}\right. \\ $$$$=\underset{{t}\geqslant\mathrm{0}} {\sum}\left({t}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{t}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {re}^{−\left({n}+{t}+\mathrm{1}\right){r}} {dr} \\ $$$$=\underset{{t}\geqslant\mathrm{0}} {\sum}\left({t}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{t}+\mathrm{1}} \int_{\mathrm{0}} ^{+\infty} \frac{{ue}^{−{u}} }{\left({n}+{t}+\mathrm{1}\right)^{\mathrm{2}} }{du}\: \\ $$$$=\underset{{t}\geqslant\mathrm{0}} {\sum}\left({t}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{t}+\mathrm{1}} .\frac{\Gamma\left(\mathrm{2}\right)}{\left({n}++\mathrm{1}+{t}\right)^{\mathrm{2}} } \\ $$$$=\underset{{t}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{t}+\mathrm{1}} \left({t}+\mathrm{1}\right)}{\left({n}+{t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *