Menu Close

Give-f-x-x-5-5x-4-4x-3-3x-2-2x-1-amp-2-1-3-5-3-3-1-3-2-1-3-5-3-3-1-3-Find-f-

Tinku Tara 0 Comments
Pin




Question Number 144327 by SOMEDAVONG last updated on 24/Jun/21
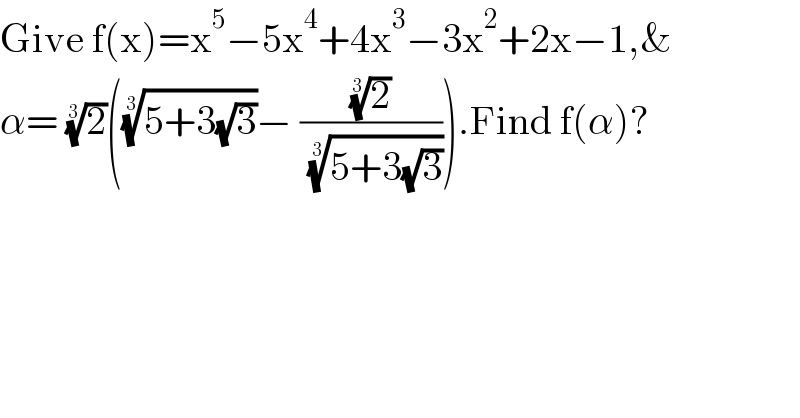
Give f(x)=x^5 −5x^4 +4x^3 −3x^2 +2x−1,& α= (2)^(1/3) (((5+3(√3)))^(1/3) − ((2)^(1/3) /( ((5+3(√3)))^(1/3) ))).Find f(α)?
$$\mathrm{Give}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{5}} −\mathrm{5x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1},\& \\ $$$$\alpha=\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}−\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}}\right).\mathrm{Find}\:\mathrm{f}\left(\alpha\right)? \\ $$
Answered by Rasheed.Sindhi last updated on 25/Jun/21
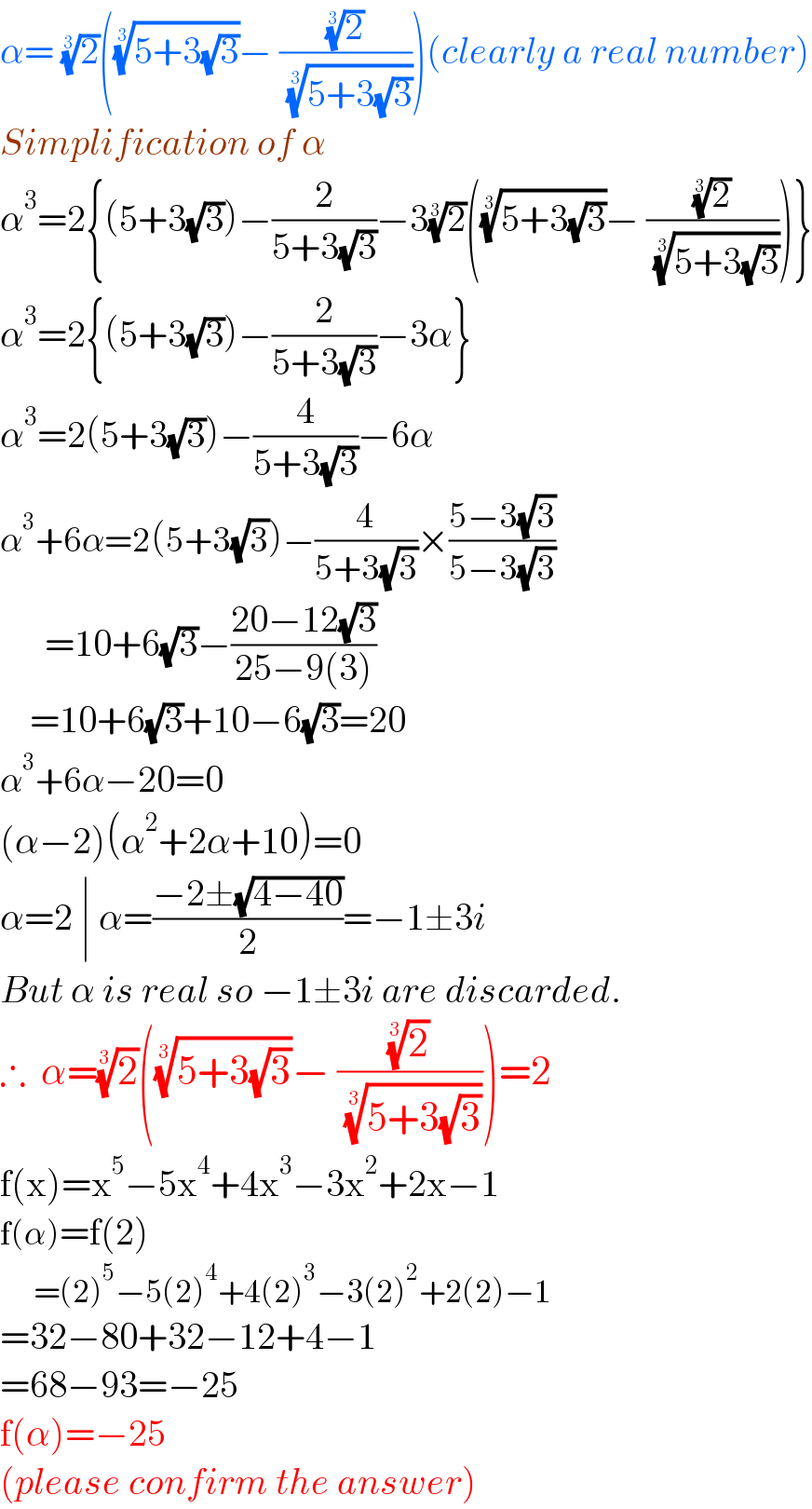
α= (2)^(1/3) (((5+3(√3)))^(1/3) − ((2)^(1/3) /( ((5+3(√3)))^(1/3) )))(clearly a real number) Simplification of α α^3 =2{(5+3(√3))−(2/(5+3(√3)))−3(2)^(1/3) (((5+3(√3)))^(1/3) − ((2)^(1/3) /( ((5+3(√3)))^(1/3) )))} α^3 =2{(5+3(√3))−(2/(5+3(√3)))−3α} α^3 =2(5+3(√3))−(4/(5+3(√3)))−6α α^3 +6α=2(5+3(√3))−(4/(5+3(√3)))×((5−3(√3))/(5−3(√3))) =10+6(√3)−((20−12(√3))/(25−9(3))) =10+6(√3)+10−6(√3)=20 α^3 +6α−20=0 (α−2)(α^2 +2α+10)=0 α=2 ∣ α=((−2±(√(4−40)))/2)=−1±3i But α is real so −1±3i are discarded. ∴ α=(2)^(1/3) (((5+3(√3)))^(1/3) − ((2)^(1/3) /( ((5+3(√3)))^(1/3) )))=2 f(x)=x^5 −5x^4 +4x^3 −3x^2 +2x−1 f(α)=f(2) =(2)^5 −5(2)^4 +4(2)^3 −3(2)^2 +2(2)−1 =32−80+32−12+4−1 =68−93=−25 f(α)=−25 (please confirm the answer)
$$\alpha=\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}−\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}}\right)\left({clearly}\:{a}\:{real}\:{number}\right) \\ $$$${Simplification}\:{of}\:\alpha \\ $$$$\alpha^{\mathrm{3}} =\mathrm{2}\left\{\left(\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}\right)−\frac{\mathrm{2}}{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}−\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}}\right)\right\} \\ $$$$\alpha^{\mathrm{3}} =\mathrm{2}\left\{\left(\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}\right)−\frac{\mathrm{2}}{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{3}\alpha\right\} \\ $$$$\alpha^{\mathrm{3}} =\mathrm{2}\left(\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}\right)−\frac{\mathrm{4}}{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{6}\alpha \\ $$$$\alpha^{\mathrm{3}} +\mathrm{6}\alpha=\mathrm{2}\left(\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}\right)−\frac{\mathrm{4}}{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}×\frac{\mathrm{5}−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{5}−\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:=\mathrm{10}+\mathrm{6}\sqrt{\mathrm{3}}−\frac{\mathrm{20}−\mathrm{12}\sqrt{\mathrm{3}}}{\mathrm{25}−\mathrm{9}\left(\mathrm{3}\right)} \\ $$$$\:\:\:\:=\mathrm{10}+\mathrm{6}\sqrt{\mathrm{3}}+\mathrm{10}−\mathrm{6}\sqrt{\mathrm{3}}=\mathrm{20} \\ $$$$\alpha^{\mathrm{3}} +\mathrm{6}\alpha−\mathrm{20}=\mathrm{0} \\ $$$$\left(\alpha−\mathrm{2}\right)\left(\alpha^{\mathrm{2}} +\mathrm{2}\alpha+\mathrm{10}\right)=\mathrm{0} \\ $$$$\alpha=\mathrm{2}\:\mid\:\alpha=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{40}}}{\mathrm{2}}=−\mathrm{1}\pm\mathrm{3}{i} \\ $$$${But}\:\alpha\:{is}\:{real}\:{so}\:−\mathrm{1}\pm\mathrm{3}{i}\:{are}\:{discarded}. \\ $$$$\therefore\:\:\alpha=\sqrt[{\mathrm{3}}]{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}−\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}}\right)=\mathrm{2}\:\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{5}} −\mathrm{5x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1} \\ $$$$\mathrm{f}\left(\alpha\right)=\mathrm{f}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:=\left(\mathrm{2}\right)^{\mathrm{5}} −\mathrm{5}\left(\mathrm{2}\right)^{\mathrm{4}} +\mathrm{4}\left(\mathrm{2}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$$=\mathrm{32}−\mathrm{80}+\mathrm{32}−\mathrm{12}+\mathrm{4}−\mathrm{1} \\ $$$$=\mathrm{68}−\mathrm{93}=−\mathrm{25} \\ $$$$\mathrm{f}\left(\alpha\right)=−\mathrm{25} \\ $$$$\left({please}\:{confirm}\:{the}\:{answer}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *