Question Number 121293 by abdullahquwatan last updated on 06/Nov/20

$$\mathrm{give}\:\mathrm{me}\:\mathrm{difficult}\:\mathrm{problems}\:\mathrm{exponent}\: \\ $$
Commented by liberty last updated on 06/Nov/20
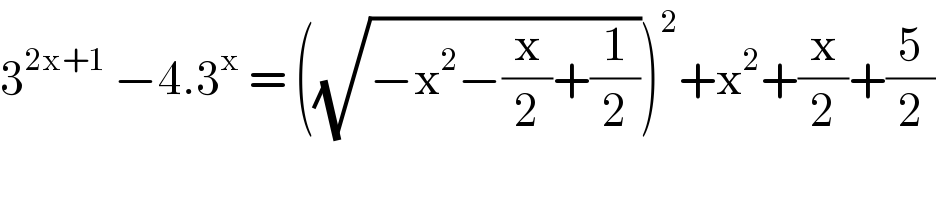
$$\mathrm{3}^{\mathrm{2x}+\mathrm{1}} \:−\mathrm{4}.\mathrm{3}^{\mathrm{x}} \:=\:\left(\sqrt{−\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Commented by liberty last updated on 06/Nov/20
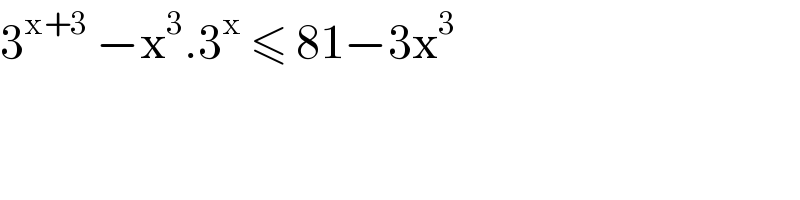
$$\mathrm{3}^{\mathrm{x}+\mathrm{3}} \:−\mathrm{x}^{\mathrm{3}} .\mathrm{3}^{\mathrm{x}} \:\leqslant\:\mathrm{81}−\mathrm{3x}^{\mathrm{3}} \\ $$
Commented by liberty last updated on 06/Nov/20
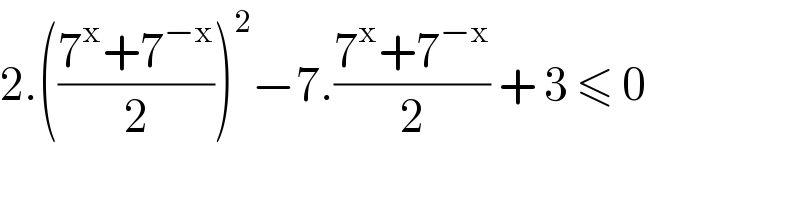
$$\mathrm{2}.\left(\frac{\mathrm{7}^{\mathrm{x}} +\mathrm{7}^{−\mathrm{x}} }{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{7}.\frac{\mathrm{7}^{\mathrm{x}} +\mathrm{7}^{−\mathrm{x}} }{\mathrm{2}}\:+\:\mathrm{3}\:\leqslant\:\mathrm{0} \\ $$
Commented by liberty last updated on 06/Nov/20
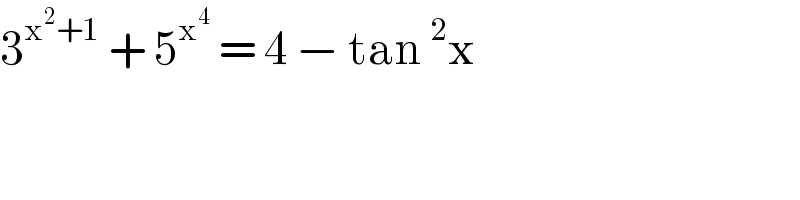
$$\mathrm{3}^{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \:+\:\mathrm{5}^{\mathrm{x}^{\mathrm{4}} } \:=\:\mathrm{4}\:−\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\: \\ $$
Commented by abdullahquwatan last updated on 06/Nov/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by talminator2856791 last updated on 06/Nov/20
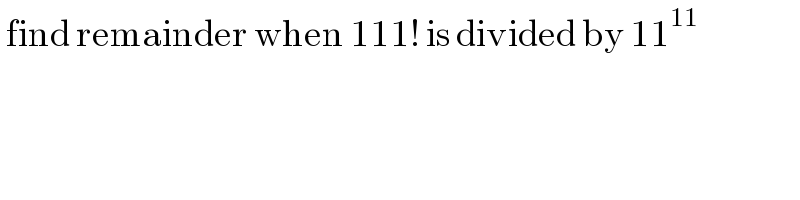
$$\:\mathrm{find}\:\mathrm{remainder}\:\mathrm{when}\:\mathrm{111}!\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{11}^{\mathrm{11}} \: \\ $$
Answered by Ar Brandon last updated on 06/Nov/20

$$\mathrm{You}\:\mathrm{can}\:\mathrm{simply}\:\mathrm{go}\:\mathrm{to}\:\boldsymbol{\mathrm{selected}}\:\boldsymbol{\mathrm{topics}} \\ $$$$\mathrm{then}\:\mathrm{choose}\:\mathrm{your}\:\mathrm{desired}\:\mathrm{topic}\:\boldsymbol{\mathrm{logarithms}}. \\ $$$$\mathrm{There}\:\mathrm{you}'\mathrm{ll}\:\mathrm{find}\:\mathrm{questions}\:\mathrm{which}\:\mathrm{may}\:\mathrm{seem}\: \\ $$$$\mathrm{interesting}\:\mathrm{to}\:\mathrm{you}. \\ $$
