Question Number 31145 by Joel578 last updated on 03/Mar/18
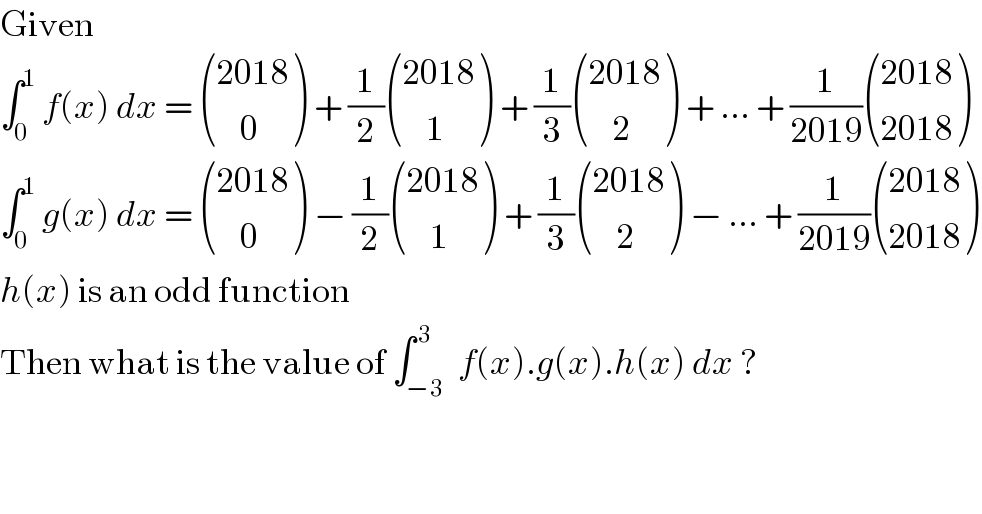
$$\mathrm{Given} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{f}\left({x}\right)\:{dx}\:=\:\begin{pmatrix}{\mathrm{2018}}\\{\:\:\:\:\mathrm{0}}\end{pmatrix}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2018}}\\{\:\:\:\:\mathrm{1}}\end{pmatrix}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{2018}}\\{\:\:\:\:\mathrm{2}}\end{pmatrix}\:+\:…\:+\:\frac{\mathrm{1}}{\mathrm{2019}}\begin{pmatrix}{\mathrm{2018}}\\{\mathrm{2018}}\end{pmatrix} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{g}\left({x}\right)\:{dx}\:=\:\begin{pmatrix}{\mathrm{2018}}\\{\:\:\:\:\mathrm{0}}\end{pmatrix}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2018}}\\{\:\:\:\:\mathrm{1}}\end{pmatrix}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{2018}}\\{\:\:\:\:\mathrm{2}}\end{pmatrix}\:−\:…\:+\:\frac{\mathrm{1}}{\mathrm{2019}}\begin{pmatrix}{\mathrm{2018}}\\{\mathrm{2018}}\end{pmatrix} \\ $$$${h}\left({x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function} \\ $$$$\mathrm{Then}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{−\mathrm{3}} ^{\:\mathrm{3}} \:{f}\left({x}\right).{g}\left({x}\right).{h}\left({x}\right)\:{dx}\:? \\ $$
Answered by ajfour last updated on 03/Mar/18
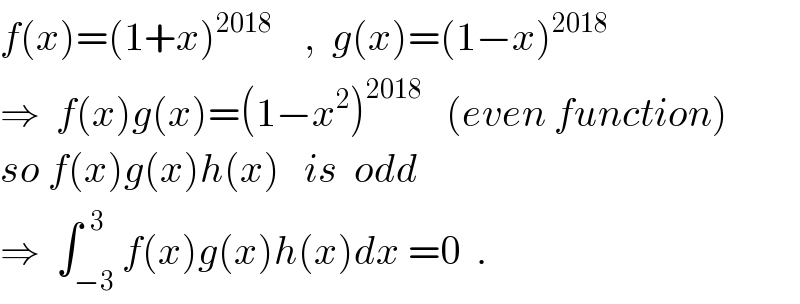
$${f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{\mathrm{2018}} \:\:\:\:,\:\:{g}\left({x}\right)=\left(\mathrm{1}−{x}\right)^{\mathrm{2018}} \\ $$$$\Rightarrow\:\:{f}\left({x}\right){g}\left({x}\right)=\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2018}} \:\:\:\left({even}\:{function}\right) \\ $$$${so}\:{f}\left({x}\right){g}\left({x}\right){h}\left({x}\right)\:\:\:{is}\:\:{odd} \\ $$$$\Rightarrow\:\:\int_{−\mathrm{3}} ^{\:\:\mathrm{3}} {f}\left({x}\right){g}\left({x}\right){h}\left({x}\right){dx}\:=\mathrm{0}\:\:. \\ $$
Commented by Joel578 last updated on 04/Mar/18
$${Thank}\:{you}\:{very}\:{much} \\ $$
