Question Number 21426 by x² – y²@gmail.com last updated on 23/Sep/17
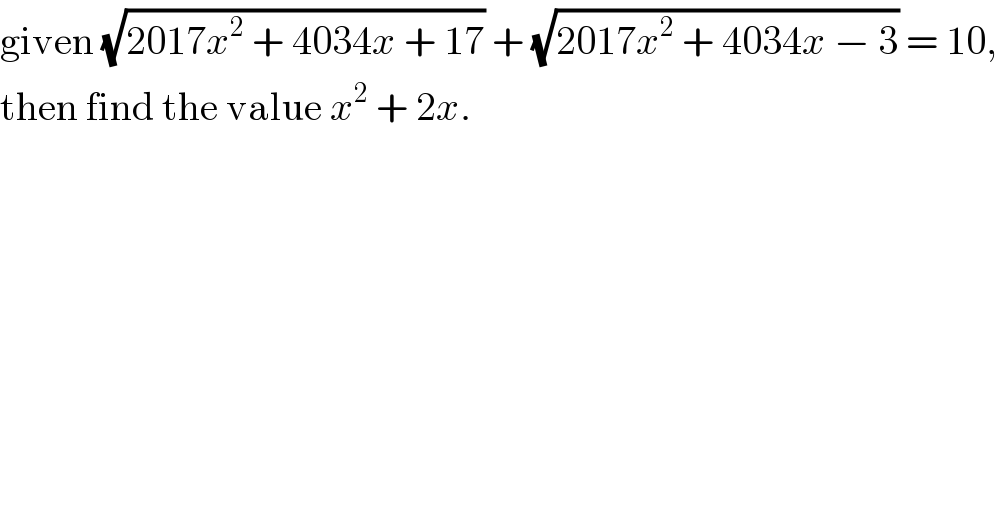
$$\mathrm{given}\:\sqrt{\mathrm{2017}{x}^{\mathrm{2}} \:+\:\mathrm{4034}{x}\:+\:\mathrm{17}}\:+\:\sqrt{\mathrm{2017}{x}^{\mathrm{2}} \:+\:\mathrm{4034}{x}\:−\:\mathrm{3}}\:=\:\mathrm{10}, \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}. \\ $$
Answered by $@ty@m last updated on 23/Sep/17
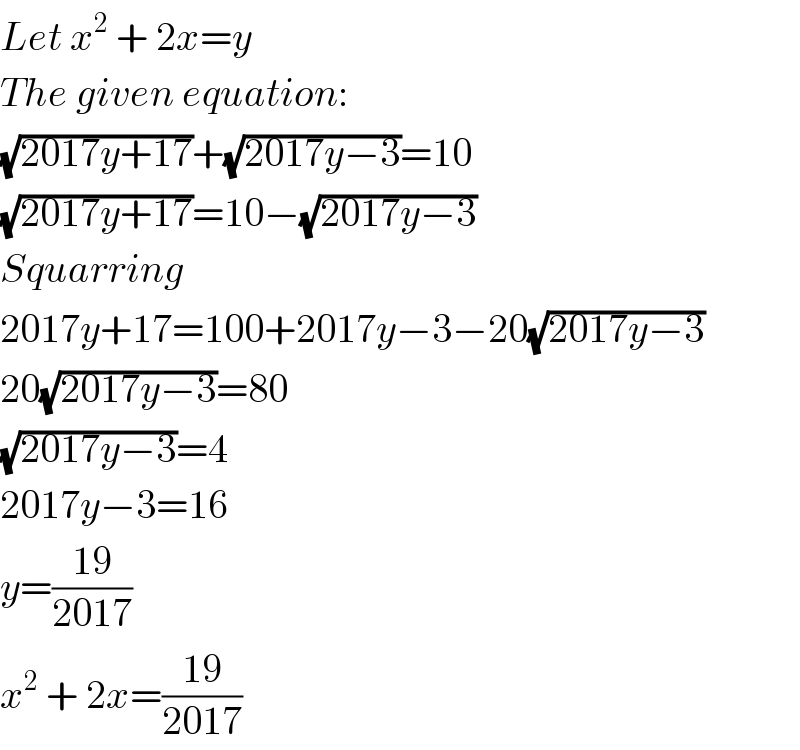
$${Let}\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}={y} \\ $$$${The}\:{given}\:{equation}: \\ $$$$\sqrt{\mathrm{2017}{y}+\mathrm{17}}+\sqrt{\mathrm{2017}{y}−\mathrm{3}}=\mathrm{10} \\ $$$$\sqrt{\mathrm{2017}{y}+\mathrm{17}}=\mathrm{10}−\sqrt{\mathrm{2017}{y}−\mathrm{3}} \\ $$$${Squarring} \\ $$$$\mathrm{2017}{y}+\mathrm{17}=\mathrm{100}+\mathrm{2017}{y}−\mathrm{3}−\mathrm{20}\sqrt{\mathrm{2017}{y}−\mathrm{3}} \\ $$$$\mathrm{20}\sqrt{\mathrm{2017}{y}−\mathrm{3}}=\mathrm{80} \\ $$$$\sqrt{\mathrm{2017}{y}−\mathrm{3}}=\mathrm{4} \\ $$$$\mathrm{2017}{y}−\mathrm{3}=\mathrm{16} \\ $$$${y}=\frac{\mathrm{19}}{\mathrm{2017}} \\ $$$${x}^{\mathrm{2}} \:+\:\mathrm{2}{x}=\frac{\mathrm{19}}{\mathrm{2017}} \\ $$
