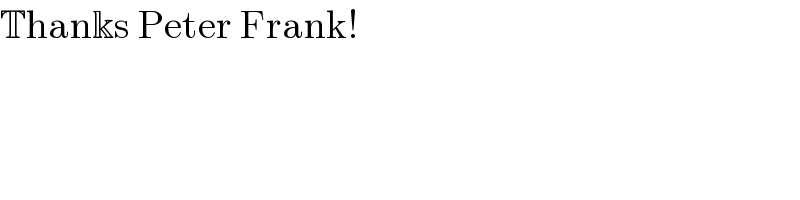given-2020-x-2020-x-3-2020-6x-2020-6x-2020-x-2020-x-

Question Number 163284 by MathsFan last updated on 05/Jan/22

g i v e n 2020^{x} + 2020^{- x} = 3

\sqrt{\frac{2020^{6 x} - 2020^{- 6 x}}{2020^{x} - 2020^{- x}}} = ?

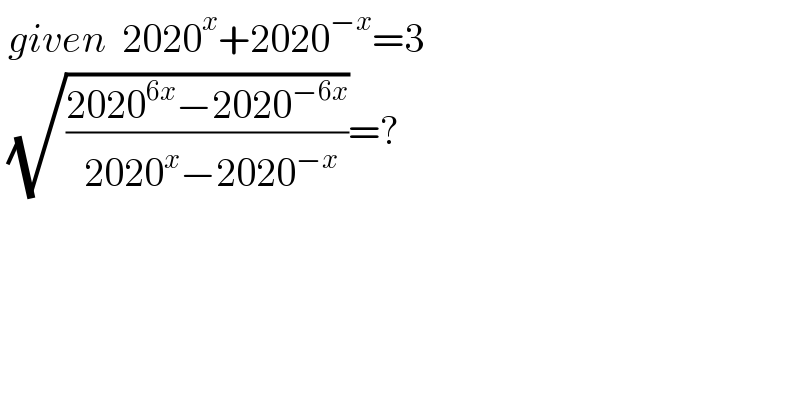
Answered by Rasheed.Sindhi last updated on 05/Jan/22

2020^{x} + 2020^{- x} = 3

\sqrt{\frac{2020^{6 x} - 2020^{- 6 x}}{2020^{x} - 2020^{- x}}} = ?

2020^{x} = y, 2020^{- x} = \frac{1}{y}

y + \frac{1}{y} = 3

{(y + \frac{1}{y})}^{2} = 9

y^{2} + \frac{1}{y^{2}} = 9 - 2 = 7

\sqrt{\frac{2020^{6 x} - 2020^{- 6 x}}{2020^{x} - 2020^{- x}}} = \sqrt{\frac{y^{6} - \frac{1}{y^{6}}}{y - \frac{1}{y}}}

= \sqrt{\frac{(y - \frac{1}{y}) (y + \frac{1}{y}) (y^{2} - 1 + \frac{1}{y^{2}}) (y^{2} + 1 + \frac{1}{y^{2}})}{(y - \frac{1}{y})}}

= \sqrt{(y + \frac{1}{y}) (y^{2} - 1 + \frac{1}{y^{2}}) (y^{2} + 1 + \frac{1}{y^{2}})}

= \sqrt{(3) (7 - 1) (7 + 1)} = \sqrt{144} = 12

Commented by MathsFan last updated on 05/Jan/22

m e r c i s e n i o r

Commented by peter frank last updated on 06/Jan/22

great

Commented by Rasheed.Sindhi last updated on 06/Jan/22

T han k s Peter Frank!